打开文本图片集

创新教育，即创新精神和实践能力的培养，是以培养学生再次发现的探索能力、“重组知识”的综合能力、应用知识解决问题的实践能力和激发创造能力为目的的一系列教育活动。它要求教师在继承教育优良传统的基础上，树立创新意识，探求创新学习的方法和途径，做学生自主学习的引导者、学生能力的培养者。数学课堂是培养学生创造精神的主阵地。本文就如何把创新教育合理、有机地渗透到初中数学课堂教学中，使其充满新的生机与活力谈三点看法。

一、改变教学观念，大胆创新

传统的课堂教学就是“传道、授业、解惑”。课堂上教师过于注重知识的传授，习惯将学生的思维活动纳入自己事先设计好的教学轨道上，而无暇顾及学生是否深度参与了课堂教学，是否在获得基础知识与基本技能的同时学会了学习，形成了正确的价值观。创新教育要求教师应改变原有的教学观念，突破传统的接受性学习方式，采用科学探究的学习方式，鼓励学生多动手、多动脑、多发现。如：苏科版九年级“黄金分割”中“黄金三角形”的推导与拓展。

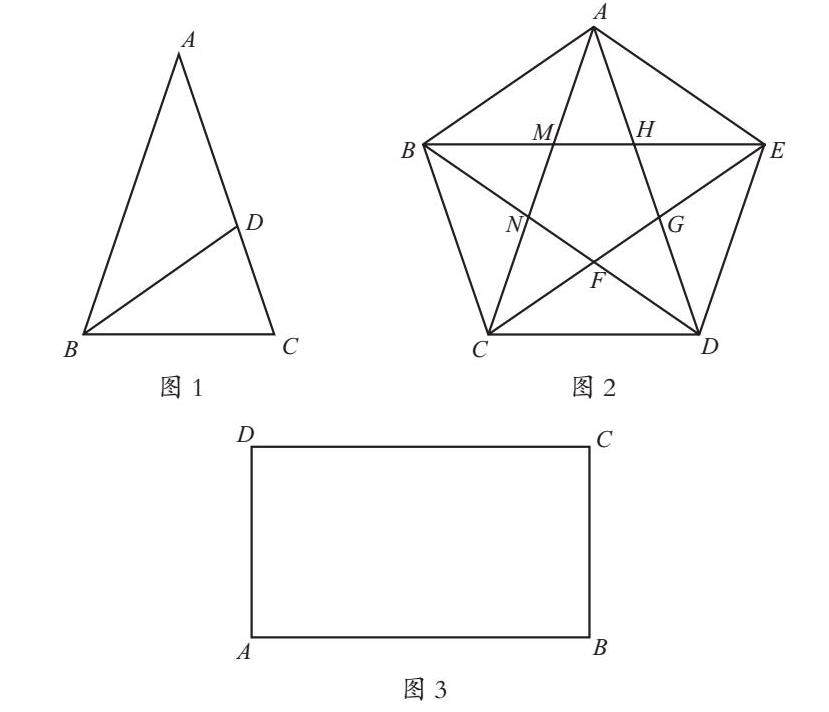
1.如图1，请你作顶角为36°的等腰△ABC，量出底BC与腰AB的长度， 计算底BC与腰AB的比值 ；

2.如图1，作∠ABC的平分线，交AC于点D，量出CD的长度，再计算CD与BC的比值 （精确到0.001）；

3.顶角为36°的等腰三角形，我们称为黄金三角形。你能归纳出黄金三角形有什么性质吗？

4.如图2，你能找出正五边形中的黄金三角形和黄金分割点吗？

5.拓展：如图3，在黄金矩形ABCD中，（1）作正方形AEFD，使顶点E，F分别在边AB，CD上；（2）分别量出矩形BCFE的边BE，BC的长度，它们的比值是否约等于0.618？重复这个过程，你能探索、归纳出黄金矩形的有关性质吗？

在整个教学过程中，教师充分尊重和相信学生的学习能力，在教学中创设宽松的学习环境，给学生思考和交流的机会，允许学生表达自己的理解，给学生足够的思维时间和空间去发现问题、提出问题和解决问题，解放了学生的头脑，让学生去想、去思考，也解放了学生的双手，给学生以动手的机会，使他们在手脑并用中发展创造力。

二、改进教学方法，勇于创新

创新教育要求教师应根据不同的教学内容、不同的教学对象灵活选择科学、合理的教学方法。问题是课堂教学的灵魂，没有好的问题设计，就没有好的教学。问题是思想方法、知识积累和发展的逻辑力量，是生长新思想、新方法、新知识的种子。巴尔扎克曾说过：“问题是开启任何一门科学的钥匙。”因此，在数学课堂教学中，我们不妨采用问题教学法。以问题为重点，让所有的学习活动都围绕问题这个核心展开。如：一元二次方程中根与系数关系定理的讲解：1.试求：一元二次方程x2+5x+6=0和x2-2x-1=0的两根，并观察你所求出的方程的两个根与方程各项系数之间有什么关系。2.由此，你对形如x2+px+q=0的一元二次方程的根与系数之间的关系有怎样的猜想？3.如何验证？4.若是二次项系数不为1的一元二次方程呢？如：2x2-3x+1=0和3x2-5x-2=0。它们的根与系数之间又存在怎样的关系呢？5.形如：ax2+bx+c=0（a，b，c为常数，a≠0）的一元二次方程根与系数之间存在怎样的关系？6.如何验证？也可采用启发式教学法。

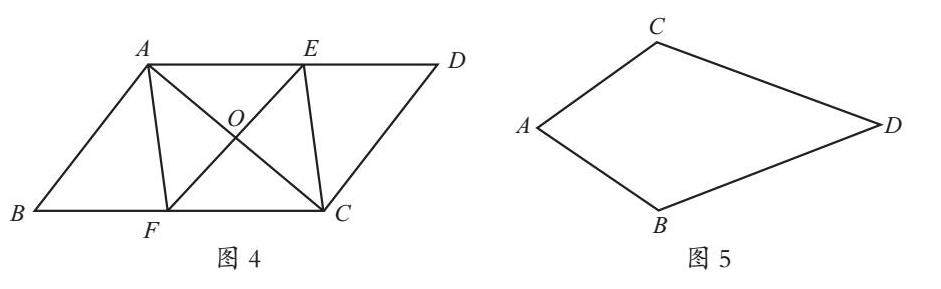
《学记》中曰：“君子之教，喻也。道而弗牵；强而弗抑；开而弗达。”即优秀的教师在教学过程中总是注重启发引导学生，使之明晓事理。引导学生而不是牵着学生走，鼓励学生而不强迫学生走，启发学生而不代替学生达成结论。如：苏科版八年级“中心对称图形（一）”中有这样的一道习题：如图4，在四边形ABCD中，AD∥BC，对角线AC的垂直平分线与边AD，BC分别相交于点E，F，四边形AFCE是菱形吗？为什么？

学生：∵EF垂直平分AC，∴根据线段垂直平分线的性质定理可知AE=EC，AF=FC，∴四边形AFCE是菱形。在这个过程中学生甲只证明了该四边形的两组邻边分别相等，与菱形的判别方法之一：“四条边都相等的四边形是菱形”并不吻合。因此，在听完学生的回答后，教师举出反例（如图5）加以说明，并引导学生关注已知条件之一：四边形AFCE的对角线互相垂直，所以要证明四边形AFCE是菱形，只需证明四边形AFCE是平行四边形，而要证明四边形AFCE是平行四边形，由于它的一组对边AE∥FC，所以只需证明AE=FC，而要证明AE=FC，只需证明这两条线段所在的两个三角形全等即可。通过这样的启发，学生很快给出了完整的解题过程。在数学教学过程中，教师应根据课堂教学的需要，选择合适的教学方法，最大限度地启发引导学生去掌握知识的生成过程，积极调动学生思维的参与，发展学生的创造技能。

三、改进教学手段，积极创新

在数学教学中融入创新教育，要求教师能采用多种现代化教学手段，积极调动学生充分参与活动，在活动中更好地理解知识、接受知识和应用知识。新教材中很多内容可以通过观看数学教学课件来直观感受。如：上例中“黄金三角形”的推导。除了让学生自己动手操作发现这种等腰三角形的底边与腰的比约等于0.618之外，教师也可借助几何画板加深学生对这类特殊三角形的感受。又如：八年级“反比例函数的图像”。同样的，可以把多个反比例函数图像在计算机上显示出来，使学生不再局限于自己尝试的几个比较特殊的反比例函数（如y=和y=-），从而能更直观形象地发现、归纳反比例函数的特征。教师应把计算机、多媒体、互联网等信息技术应用到位，为学生提供探索复杂问题、多角度思考问题的机会，从而加深学生对学习内容的理解，拓宽学生的学习领域，发展学生的个性与创新精神。

初中生的思维正处于以具体形象思维为主要形式向以抽象逻辑思维为主要形式逐步过渡的阶段，数学知识的抽象性与学生认识的具体现象之间存在着矛盾。在教学中教师要根据学生这一年龄段的特点，抓住数学学科特点，不断鼓励、引导学生在探求知识的过程中培养创新精神，形成创新思维和能力，并最终让创新教育成为习惯。