打开文本图片集

摘要：本文呈现“全等三角形之手拉手模型”主题复习课的教学过程，立足于“一题、一类、一课”的新课标主题活动设计思路和理念，注重基础知识、基本方法、基本图形与基本结论的有机重构，挖掘教材习题进行改编，加强知识间的联系，让学生在课堂上进行深入全面的探究，力求核心素养在课堂上落地.

关键词：一题一课  手拉手模型  主题复习 核心素养

《义务教育数学课程标准（2022年版）》（以下简称新课标）明确提到“教师在教学中要引导学生在数学概念、 原理和法则之间构建起有效的认知结构，体会不同教学内容之间数学研究方法的一致性和可迁移性，帮助学生学会用整体的、联系的、发展的眼光看问题，形成科学的思维习惯，发展数学核心素养”[1]. 在素养立意的新课标视角下，笔者基于“一题一课”模式设计了“全等三角形之手拉手模型”主题复习课.深入探究题目本质，抓住图形特征，在问题解决中发展思维能力，在变式探究中提升迁移能力，在归纳总结中提炼解题经验.

1.教学过程设计

1.1感知模型 探索性质

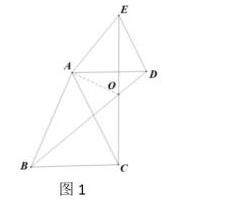
如图1，AB=AC，AD=AE，∠BAC=∠DAE=α，在△ADE绕点A旋转的过程中，你能获得哪些结论？并简述证明过程？

（教师让学生上讲台展示探究成果......）

师：经过刚才的探究，我们归纳一下该模型的特征与性质.

师生共同归纳：如图1中双等腰，共顶点，顶角相等具有这样特征的图形，可将BD，CE称为拉手线，这个几何图形可称为手拉手模型.它具有如下四组常用性质：

△ABD≌△ACE；

拉手线等长BD=CE；

拉手线的夹角等于顶角∠BOC=∠BAC=∠DAE；

AO平分∠BOE

【设计意图】该环节让学生自主证明“手拉手模型”具有的4组基本性质，在学生给出证明的过程中加深了对性质的理解和记忆，为后续应用该模型解题作了铺垫.该教学环节旨在建立数学模型观念，探索模型性质，而不是生硬记忆模型性质.

1.2熟悉模型 加深认识

学生练习

根据等腰三角形共顶点的手拉手模型，请直接写出相应的结论：

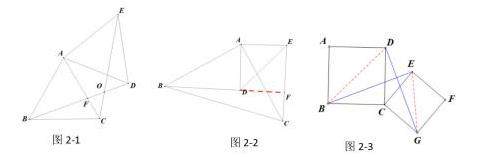
1、如图2-1△ABC和△ADE均为等边三角形

2、如图2-2△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝900

3、如图2-3四边形ABCD和四边形CEFG均为正方形

【设计意图】：该教学环节使学生对“手拉手模型”的几个基本结论有了更深刻的认识和更系统的了解，让学生感受手拉手问题中“图形变换，全等不变的本质”.同时体会数学从一般到特殊的的思想.教师通过利用几何画板动态演示，促进学生对变化中不变的理解.

1.3运用模型 构造模型

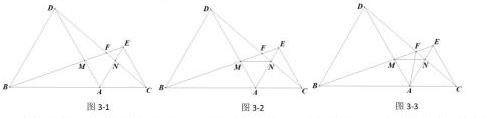
如图3-1，△ABD和△AEC都是等边三角形，将△AEC绕点A旋转过程中，当点A、B、C三点共线时，连接BE、CD 交点为点F，分别交AD、AE于点M、N.

（1）从图形变化的角度说明△EBA可以看做是△CDA怎么变化得到.

（2）如图3-2连接MN，请判断△AMN的形状.

（3）图3-3，连接AF，求证FB=FD+FA.

【设计意图】本题源于（人教版《数学》九年级上册第76页习题改编），此教学环节是“手拉手模型”的深层次挖掘，三个小问的设计考查运用模型、构造模型，难度由易到难，递推跟进.学生掌握了“手拉手模型”的特征以及能构造全等三角形基础上，建立复杂几何图中的边、角关系.本环节培养了学生几何直观，模型观念，推理能力等数学核心素养.

1.4 归纳总结 提炼升华

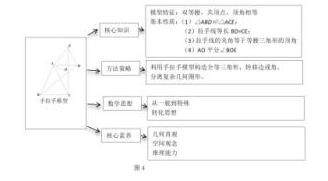
师生共同归纳小结本节课的核心知识，数学思想，数学素养.将本节课的内容用思维框图呈现，如图4.

2.教学反思

复习课开展普遍用时长且效果差，通过本节课的的实践，旨在通过主题复习课的方式找到一类问题的通性通法，进而会一题通一类达到主题复习的辐射性.

2.1挖掘模型本质，寻求解题策略

几何问题通常由基本图形或基本几何模型构成，掌握了这些基本图形或基本几何模型及相关性质，就能够解决一般的几何问题.在实际数学问题中，一些基本图形通常需要经过转化或构造等方式才能显现出来，这就要求平时在教学中要强化学生识图，析图的训练.通过一题多解，一题多变，培养学生思维迁移能力，鼓励学生深度挖掘几何模型的基本特征，进而归纳数学解题的基本策略.

2.2整合教材，形成专题

教材要发挥“启智增慧，培根铸魂”的作用，教师就必须充分挖掘教材中的资源，加强知识间的相互联系[2].本节课是人教版八年级上册第十二章《全等三角形》和九年级上册第二十三章《旋转》的整合内容.“全等手拉手”模型在探究类的压轴数学题中经常作为基本图形出现.本教学设计中的“运用模型，构造模型”教学环节，通过挖掘教材中相关习题，进行改编有一定意义.学生在探索过程中能提升自己的数学抽象能力、逻辑推理能力、几何直观能力、数学建模能力.从而使学生的数学学科核心素养得以发展.

2.3重视信息技术的运用

《义务教育数学课程标准（2022年版）》在“教学建议”中指出，教师可以利用信息技术对文本、图像、声音、动画等进行综合处理，丰富教学场景，激发学生学习数学的兴趣和探究新知的欲望[1].教学环节中教师通过几何画板演示：改变“手拉手模型”中两等腰三角形旋转的角度，等腰三角形顶角的度数，在通过几何画板中的度量工具可以验证出两条拉手线的长度在变化过程中始终相等，且夹角始终等于等腰三角形的顶角.几何画板的运用将几何图形的动态变化直观化、形象化，促进学生对变化中不变的理解，逐步形成几何直观.

参考文献

[1]中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

[2]崔允漷. 如何开展指向学科核心素养的大单元设计[J].北京教育（普教版）2019（2）：11-15.

[3]吴立建.“一题一课”理念下的教学实施[J].江苏教育（中学教学版），2018（2）：26-28