打开文本图片集

摘要：针对平均行程速度受多种因素影响、随机性强且波动性大的问题，提出了一种基于集合经验模态分解法（EEMD）、动态时间归整法（DTW）和长短时记忆神经网络（LSTM）的组合预测模型。将不平稳的序列分解为相对平稳的周期序列和趋势序列；再利用动态时间规整法度量各分量与原始数据之间的相关性，将不同分量组合并添加降雨量、能见度等辅助变量作为长短时记忆神经网络的输入，叠加各分量组合预测结果作为最终的预测结果。以重庆市包茂高速渝湘段路段平均行程速度实测数据进行验证，与传统模型相比，本文构建的组合模型在提升路段平均行程速度预测精度方面具有有效性。

关键词：智能交通；平均行程速度预测；长短时记忆神经网络

中图分类号：U491; TP18                  文献标志码：A

0 引言

高速公路路段平均行程速度预测可以为交管部门制定主动管控，出行者规划最佳的出行时间和路线提供决策依据。随着机器学习算法在交通领域应用的不断深入，已有大量学者将循环神经网络（RNN）[1]、长短时神经网络（LSTM）[2-3]等算法运用于交通流参数预测中。张阳[5]、万玉龙[6]等人在改进小波分解的基础上对交通流序列进行分解，结合神经网络构成组合模型实现短时交通流的预测。冯腾[7]将经验模态分解法（EMD）与ARIMA、LSTM等模型构成组合模型，提升了交通流参数预测精度。

本文在上述研究的基础上，提出一种基于EEMD-DTW-LSTM的路段平均行程速度组合模型通过DTW算法对各分量与原始序列间的相关性进行度量，将分量组合重构并加入气候条件、道路线形等一系列辅助变量作为LSTM的输入，实现对高速公路路段平均行程速度的准确预测。

1 方法及原理

1.1 集合经验模态分解EEMD

集合经验模态分解法（（EEMD））是为了解决经验模态分解法（EMD）分解过程中经常会遇到的一个IMF分量中包含不同时间尺度分量即模态混叠现象而提出的改进算法，具体步骤如下：

（1）在目标信号序列中加入高斯白噪声生成新的序列。

（2）确定序列的所有局部极值点，将所有局部极大值点和极小值点分别用一条曲线连接构成上包络线和下包络线。取上下包络线的平均值记为，并计算和之间的差值记为。

（3）判断是否满足IMF的要求。若满足，将作为第1个IMF分量，并以剩余量来替代，并重复步骤2直到为单调函数或小于某固定值时，完成分解。

（4）分解后的原始序列可以表示为n个IMF分量与剩余量的和。

1.2 动态时间归整算法DTW

EEMD分解后得到的分量与原始信号序列之间的相关性存在差异，本文利用动态时间规整算法（DTW）度量分量与原始序列间的相关性。DTW将序列在时间上进行局部的拉伸或压缩调整，计算出时间不同步的序列之间的最小距离，以更好地表征这类序列的形态相似性。所有配对点的累加距离就用来表示两条轨迹的相关程度。

1.3 长短时记忆神经网络LSTM

长短时记忆神经网络LSTM可以看作是递归神经网络（RNN）的一种特殊结构它能够捕获具有长时间依赖性的时间序列输入，与传统的RNN类似，LSTM可以通过在不同时间戳以递归的方式连接隐藏层来捕获变量之间的时间依赖关系。记忆单元内包含输入门、遗忘门、输出门和记忆细胞，其中三个门用于控制下一个时间步骤中添加或删除的历史信息。

2模型构建

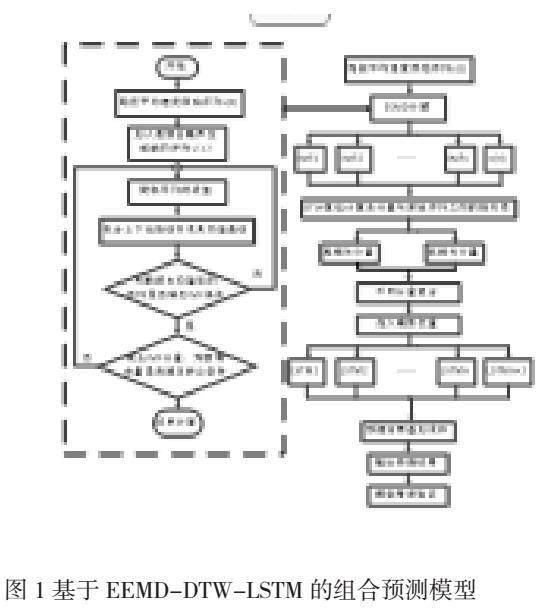
本研究构建了基于EEMD-DTW-LSTM组合预测模型提高路段平均行程速度的预测精度。思路包括：原始分量分解、分量相关性度量及分量组合重构、辅助变量加入及模型训练预测。

2.1 辅助变量选择

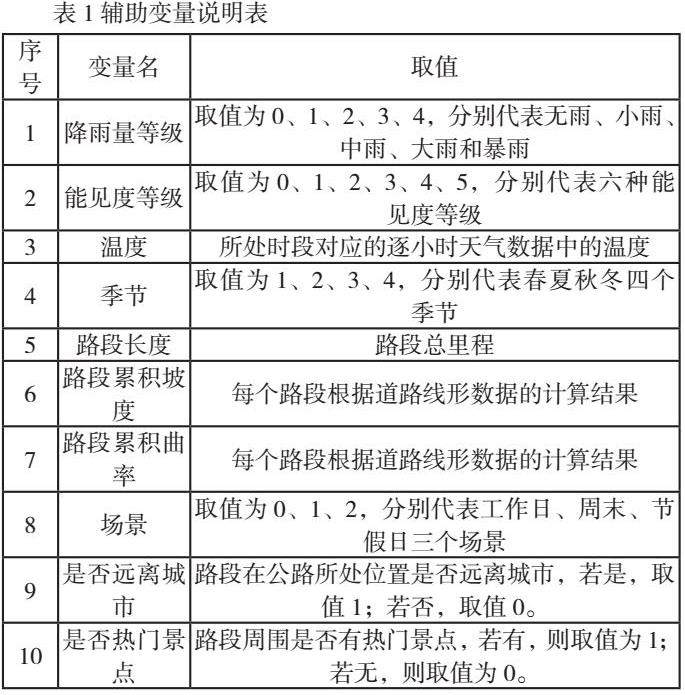
考虑高速公路路段平均行程速度受多重因素叠加影响，本文选取气候因素、道路线形因素、时间场景因素和空间因素等共10个变量作为辅助变量，具体辅助变量及取值规则如表1。

2.2 基于EEMD-DTW-LSTM的预测模型

本文构建的基于EEMD-DTW-LSTM组合模型预测的具体步骤如下所示：

Step1：对原始路段平均行程速度数据集进行预处理后构成原始序列。

Step2：利用EEMD算法对原始平均行程速度序列进行分解，得到n个IMF分量和1个剩余量，分别为IMF1、IMF2、…、IMFn-1、IMFn和Res。

Step3：利用DTW算法计算各分量序列与原始序列间的相关度，按数值大小降序排列n个IMF分量计算得到的n个相关度，将分量分为高相关分量和低相关分量两类。

Step4：将不同分量组加入辅助变量，对数据进行归一化处理并划分划分训练集和验证集。

Step5：LSTM模型搭建，确定模型中各项参数，将归一化后数据输入模型进行训练学习。

Step6：各分量预测结果叠加求和作为最终的预测结果输出。

Step7：设计多组对比实验进行预测，分析比较多组实验的预测结果与误差，对模型评价。

3 实验分析

3.1 实验数据集

本文所用的实验数据集以重庆市G65包茂高速渝湘段某路段为研究对象，针对该路段每隔5min采集一次路段平均行程车速，选取2023年6月工作日和周末两场景下的数据构造数据集，并按照7：3的比例划分训练集和测试集，对三类数据进行清洗及预处理工作，并进行时间匹配和空间匹配后构成综合数据库。

3.2 数据分解和分量相关性度量

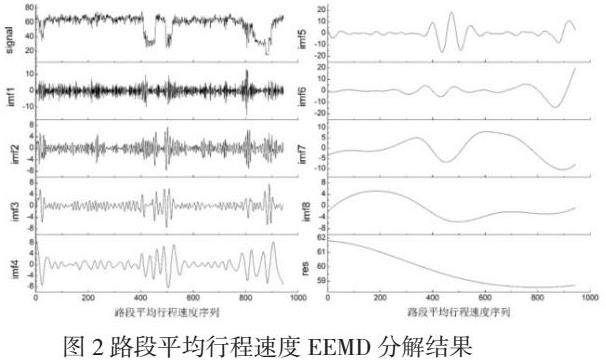
利用集合经验模态分解法（EEMD）对工作日场景下路段平均速度原始序列进行分解，结果如图3所示。原始序列中受噪声数据的影响波动明显，经EEMD分解后得到的各分量振动周期呈增长趋势，振幅逐渐降低。图2中9个分量与原始序列的相关性存在一定差异，为进一步探究各分量与原始序列之间的相关性，本文利用动态时间规整算法（DTW）度量分量与原始序列间的相关性，并根据度量结果将分量分为高相关性分量和低相关性分量两类。

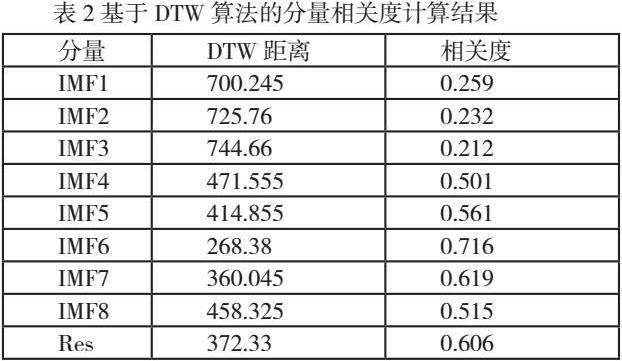
按DTW算法计算步骤分别计算各分量与原始序列之间的DTW距离，具体数值如表2所示。分解得到的9个分量中IMF4、IMF5、IMF6、IMF7、IMF8和Res这6个分量与原始序列的相关度明显高于前3个分量。因此将IMF4、IMF5、IMF6、IMF7、IMF8和Res作为高相关分量，IMF1、IMF2、IMF3作为低相关分量。

3.3 模型评估与参数设置

本文构建的组合模型中LSTM模型中包含两个LSTM层，每层Dropout比率设置为0.2，输入层神经元个数为11，输出层神经元个数为1，每层隐藏层神经元个数为20。本文采用三种评价指标：平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、均方根误差（RMSE）。

3.4 实验结果

（1）不同时间场景下预测结果对比

为验证本文设计的组合模型在多个时间场景下的普适性，将工作日和周末数据集分别输入EEMD-DTW-LSTM模型中，两个时间场景下的预测结果评价指标值如表3所示。工作日和周末场景下路段评价行程速度预测的平均绝对百分比误差MAPE分别为6.13%和8.52%。

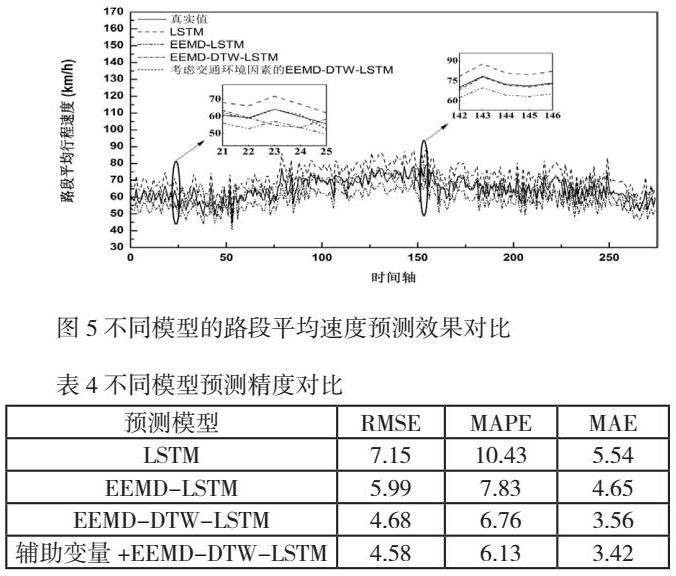
（2）不同模型预测结果对比

四组实验的预测效果对比如图5所示，结合表4中三种评价指标的计算结果，加入辅助变量的EEMD-DTW-LSTM组合模型较EEMD-LSTM模型、EEMD-DTW-LSTM组合模型和单一LSTM模型在RMSE、MAPE、MAE三项指标计算值均有所降低，预测模型中加入辅助变量后的EEMD-DTW-LSTM模型预测精度最高。根据上述实验验证了本文构建的组合模型相较于传统模型在预测精度和普适性两方面都表现较优。

4结论

（1）本文提出了基于EEMD-DTW-LSTM的高速公路路段平均行程速度组合预测模型一定程度上降低了噪声数据对预测结果的干扰。研究结果表明，将原始序列分解重构后进行预测，组合模型预测精度明显高于传统模型。

（2）以包茂高速渝湘段中路段实测数据为例，对比多组模型的预测结果发现，加入辅助变量后的EEMD-DTW-LSTM模型预测精度最高，相较于LSTM模型、EEMD-LSTM模型、EEMD-DTW-LSTM模型MAPE分别降低了4.3%、1.7%和0.63%。

参考文献

[1]王祥雪，许伦辉.基于深度学习的短时交通流预测研究[J].交通运输系统工程与信息，2018，18（01）：81-88.

[2]MA X，TAO Z，WANG Y， et al. Long short-term memory neural network for traffic speed prediction using remote microware sensor data[J]. Transportation Research Part C，2015（54）：187-197.

[3]陆文琦，芮一康，冉斌，谷远利.智能网联环境下基于混合深度学习的交通流预测模型[J].交通运输系统工程与信息，2020，20（03）：47-53.

[4]张阳，杨书敏，辛东嵘.改进小波包与长短时记忆组合模型的短时交通流预测[J].交通运输系统工程与信息，2020，20（02）：204-210.

[5]万玉龙，李新春，周红标.基于WPD-PSO-ESN的短期交通流预测[J].公路交通科技，2019，36（08）：144-151.

[6]冯腾. 基于EMD和GS-SVM融合的节假日高速公路交通流预测研究[D].长安大学，2016.