
- 收藏
- 加入书签
基于粒子群优化算法的交通流量管控问题研究
摘要:本文根据已知车流量信息数据研究了某小镇知名景区交通流量管控问题。首先通过Kmeans聚类算法将一天划分为六个时间段,并估计不同时间段四个方向的直行和转弯的车流量。其次,基于韦斯特理论对信号灯时间进行优化配置,借助粒子群优化算法求得最优信号灯配置方案,使得车辆能正常通行且最大程度上提高两条主路上车流平均速度。最后,对五一黄金周期间数据进行筛选,判定寻找停车位的巡游车辆,并在节约成本的基础上计算出满足需求的景区临时征用停车位数量。
关键词:车流量;K—means聚类;韦斯特理论;粒子群优化算法
中图分类号:U491.51 文献标识码:B
1 问题背景
随着城市化进程的加快和机动车保有量的增加,城市交通拥堵问题日益严重。研究交通流量管控问题对于缓解交通拥堵、保障交通安全等方面都具有重要的现实意义。本文研究问题背景为2024年高教社杯全国大学生数学建模竞赛题目E题[1]:交通流量管控。
问题描述:已知一小镇知名景区周边道路上通行车辆较多,其中包括本地居民出行车辆、过境车辆和前来旅游游客车辆。因游客对本地不熟悉,时常在周边徘徊寻找停车位,导致道路通行效率降低。附件1为路段行驶方向编号及交叉口之间的距离;附件2为纬中路各交叉口车辆信息;附件3为五一黄金周期间交通管控措施。为解决道路通行问题,提高通行效率。本文结合问题背景和附件有关数据,拟解决以下三个问题:
1.根据车流量的差异,将一天分为若干时间段,针对经中路——纬中路交叉口,估计不同时间段四个方向的直行和转弯的车流量。
2.基于问题1的数据和模型,优化经中路和纬中路上所有的交叉口信号灯,使得车辆能正常通行且最大程度上提高两条主路上车流平均速度。
3.分析五一黄金周期间数据,判断前来景区游览的游客车辆;为使车辆顺利停靠采用景区临时征用停车位的措施,即估计需临时征用多少停车位才能满足需求。
2 时间段划分与四个方向车流量的分析估计
2.1 经中路——纬中路交叉口四个方向各时间段车流量分析
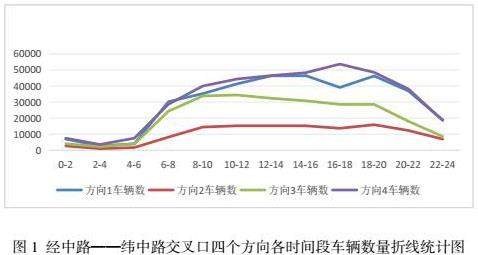
首先对一天中的车辆信息分时间段进行简单划分,研究纬中路与经中路交叉口不同时间段的车流量情况,根据附件2筛选出经中路——纬中路交叉口车流量信息,为保证结果足够精确本文细化分组区间,以2个小时为一个时间段进行车辆信息汇总,将一天中的数据分为12个时间段,为研究问题方便分别对不同时间段用数字进行标注,例如时间段“0—2”记为代号“1”,时间段“2—4”记为代号“2”,...,依次得到12个时间段及其代号。对方向1、2、3、4中经中路——纬中路交叉口所有车辆,按照时间段进行汇总。首先,将时间数据拆分为年、月、日和具体时间点,然后对车牌号进行计数汇总,得到各个时间点的车辆数量,最后以2个小时为时间段,分别汇总一天的数据情况,得到每个时间段(两小时为一个时间段)的车流量总和。首先对附件2数据进行处理,筛选出经过经中路——纬中路交叉口的所有车辆数据,统计不同时间段各个相位车辆数并绘制折线统计图(图1)。
2.2根据车流量的差异性进行时间段划分
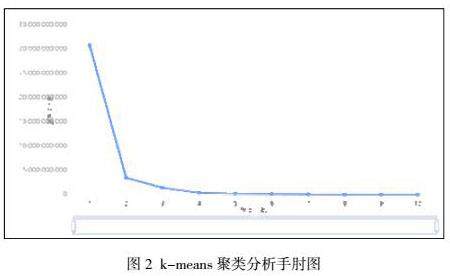
为进一步根据不同时间段车流量差异合理划分时间段,采用k-means聚类算法[2]对划分的12个时间段进行聚类分析,运用spss对一天中不同时段车流量进行k-means聚类结果图2所示。
图2的聚类结果横坐标是聚类个数,纵坐标是K-means聚类的损失函数是所有样本到类别中心的距离平方和(即误差平方和)。根据聚类结果可以看出,当聚类个数达到6时,此时聚类形态基本趋于稳定,表示在此点之后,继续增加聚类个数对提升聚类效果的贡献边际递减。因此可以确定最佳的聚类个数为6,此时既保证了聚类效果的良好性,又避免了过度聚类带来的复杂性增加。根据车流量数据最终确定的时间段划分为6段更符合实际,分类后的时间段如表1所示,按照该分类结果划分时间段能够较好地分出不同时间段的差异性。据此将一天中的数据分为6个时间段,并分别对分类后的不同时间段用数字进行标注,例如,类别2对应“时间段1、2、3”(即0~6时)记为代号“1”;类别1对应“时间段4”(即7~8时)记为代号“2”,...,依次得到6个时间段及其代号。
2.3 各时间段四个方向的直行和转弯车流量估计
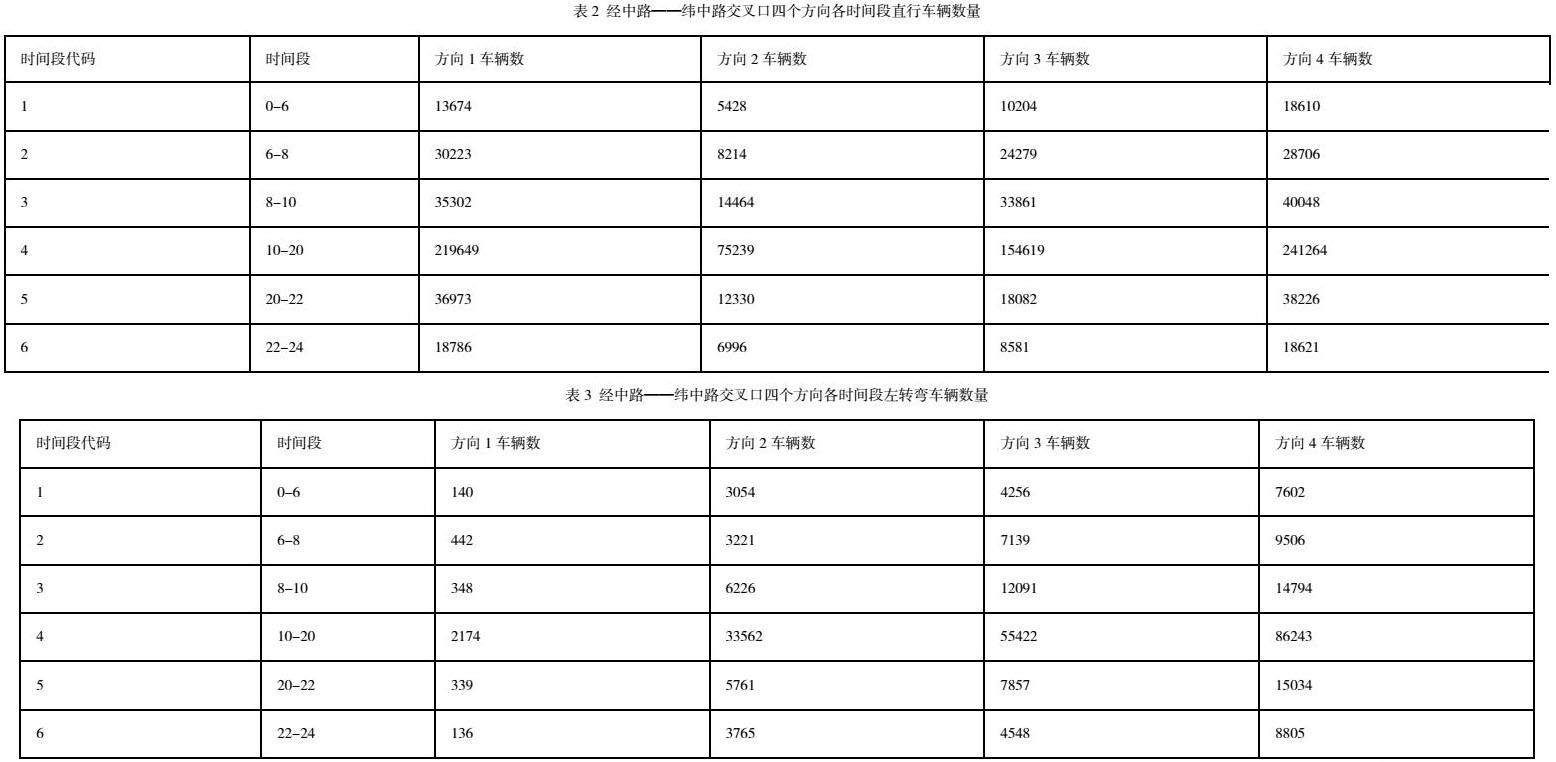
首先对数据进行预处理,剔除无车牌的数据。在研究经中路——纬中路交叉口不同时间段内车辆转弯行为的差异时,本文基于附件2处理后的数据进行分析,首先对数据进行计数统计,然后查找识别相同车辆在不同时间段和不同行驶方向的数据,判断车辆是否在经过经中路——纬中路交叉口进行转弯,例如:若车辆在驶入经中路——纬中路交叉口前,其行驶方向为方向4,经过交叉口后行驶方向不为方向4,则可以判断该车辆通过此交叉口进行了转弯行驶,否则认定为直行。最后根据交叉口总车流量数据,统计不同时间段经过经中路——纬中路交叉口各个相位的直行和转弯车辆数量,得到直行车辆数量如表2,以左转为例的转弯车流量如表3所示。
3 基于粒子群优化算法的信号灯配时优化模型建立与求解过程
3.1 基于韦伯斯特理论的交通信号灯的配时优化模型建立过程
根据问题1分时段分析结果可知,同一交叉口一天中不同时间段车流量有明显差异,在对交叉口信号灯进行优化配置时,如果全天采用统一定时控制系统,显然不符合实际需求。为此本文构建信号灯的分时段定时控制系统。为保证车辆通行的前提下,使得两条主路上的车流平均速度最大,把延误时间作为目标优化目标,采用粒子群优化算法[3],分别求取最优目标值,选择最优方案对信号灯配时进行优化,以达到提高通行效率,缓解交通压力的目的。
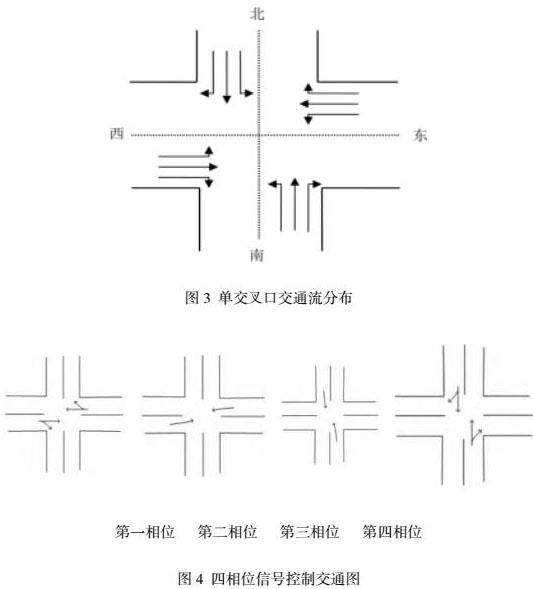
根据问题情形,该问题模型的单交叉口的交通流如图3所示。对于每个方向均有三个车流,按照研究问题实际来看,交叉路口的四个方向普遍采用四个相位做法,如图4所示。
基于交通信号灯的配时优化控制理论以韦伯斯特提出的理论最为经典,针对问题2本文以韦伯斯特理论为研究基础,对信号灯配时优化和有关参数进行求解。韦伯斯特理论认为因交通信号灯的延误时间是影响通行效率的关键,并提出了计算交叉口包含数个相位车辆的平均延误(1)和随机延误公式(2),并在此基础上给出了交叉口定时信号灯控制车辆延误的修正简化计算公式即公式(3),
其中,C为周期时间,即信号灯循环一次用到的时间,为红、黄、绿灯时间之和;为绿信比;为车道流量比,为实际车流量,为饱和度;为平均延误时间,为随机延误时间。
而问题所讨论的延误时间应为一个周期内进入交叉口所有车辆的总延误时间之和,并将此值选取的最小值作为优化目标,最终总延误时间[4-5]D的公式如(4)所示,
其中,C为周期时间,为第个相位的绿灯时长,为车道流量比,为交叉口进口实际车流量,为第个相位的车辆到达率,为饱和度,即。
3.2 基于粒子群优化算法的模型求解过程
对式(4)进行求导以及近似计算后,得到交通信号灯的最佳周期为,以总延误时间构建优化函数如式(5)所示。
其中,和表示第个相位的最小和最大绿灯时长,表示第个相位的延误时间,表示最大周期时间,表示交叉口的最大车辆饱和度。
粒子群优化(PSO)算法作为一种通过迭代的方式优化目标函数,求得最优解的计算方法。对解决规划问题有广泛应用,基于上述问题分析,本文,构建粒子群优化算法的基本流程包括,初始化粒子群,即随机选取一组数据作为初始化粒子,并随机生成粒子群的规模(即粒子的个数)和粒子的初始位置和速度,通过计算该组粒子的性能优劣进行筛选,进一步更新不同粒子的位置和速度,重复评估更新数据,经过迭代直至选出个体最优和全局最优,以及更新粒子的速度和位置。以问题一中数据为例,求经中路与纬中路交叉口方向1(由东向西)、方向2(由西向东)、方向3(由南向北)、方向4(由北向南)的四个相位对应的平均交通量,分别为0.45、0.47、0.66、0.54,并假设各个相位的饱和度和车道流量比均达到最大值,按照国家交通信号灯设置规则,人行经过时间一般不低于15s,即绿灯最低时限为15s,由此推算出信号灯最短周期时间为72秒可得最终的优化值,而交通信号灯设置时间一般不高于4分钟,由此得到基本参数的合理范围,通过粒子群优化算法计算目标函数(6)在约束条件下的结果如表3所示。
结果分析,由粒子群优化算法结果,可知对于经中路与违中路交叉口的信号灯进行优化配置时,信号灯周期总时长设置为137s较为合适,对于方向1(由东向西)、方向2(由西向东)、方向3(由南向北)、方向4(由北向南)等四个相位的绿灯时间分别设置为27s、47s、50s和35s较为合适。同理可分别求得不同交叉口各时间段的信号灯优化情况。
4 五一黄金周期间游客车辆判别与临时征用停车位估算
4.1 五一黄金周期间游客车辆判别过程
根据附件3提供的管控措施方案:车辆应按照规定的进出路线行驶。则车辆沿进入小镇景区的路线行驶可分为三种情况:
(1)车辆从未经过环东路——纬中路交叉口:因若想要前往景区或离开景区必须经过环东路——纬中路交叉口,故未经该交叉口则表明在路过此交叉口之前已寻找到停车位,后续下车再度前往景点。
(2)车辆仅经过一次环东路——纬中路交叉口:若经过该交叉口,由于小镇景点的管控措施要求只能沿规定进出口路线行驶。则需要继续开车向北行驶,并按照规定路线经过经四路——纬中路交叉口,此时车辆面临着左转右转问题。若左转(向东行驶)则说明该车在经四路——纬中路和环东路——纬中路的交叉口之间的路程内找到了停车位。若向右转(向西行驶)则说明该车辆在后续的路途中找到停车位或该车辆因未找到停车位而离开。
(3)车辆经过两次或两次以上环东路——纬中路交叉口:因管控所致,车辆并不能沿车辆驶入景区的道路驶出景区,即由附件3图中所示只能返回一小段。则车辆两次经过环东路——纬中路交叉口一定为第一次经过到第二次经过前未找到停车位,才会两次或两次以上路经该交叉口。即可判断该车已经在巡回行驶找停车位。
则可根据以上描述判定经过两次或两次以上环东路——纬中路交叉口的车辆是巡回车辆。
4.2 五一黄金周期间需临时征用停车位数量估算
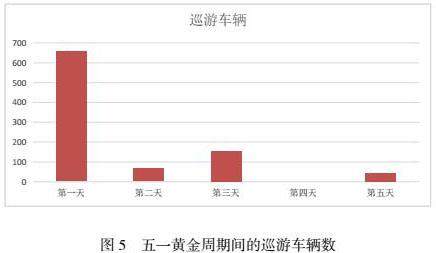
基于上述分析,根据已有数据得出每个车牌号经过环东路——纬中路交叉口的个数,选择两次及两次以上经过该交叉口的车辆,并对此进行计数处理,可求得五一黄金周期间的巡游车辆总数(如图5)。由图可知五一黄金周第一天(2024年5月1日)巡游车辆的数量远远高出另外四天的巡游车辆个数,因此停车位若能满足第一天的需求量,则后续四天也均可满足。
针对五一黄金周第一天的数据将时间进行排序,车流量主要集中在7点——9点和18点——20点两个时间段,因此根据这两个时间段对巡游车辆进行筛选,满足这两个时间段停车需求即可全天停车需求。计算得到7点——9点和18点——20点通过环东路——纬中路交叉口的车辆分别为411辆和245辆。因此,对于五一黄金周第一天,为了确保能够完全满足游客对停车位的需求,选择两个时间段中数值较大结果,应征用411个停车位。而对于五一黄金周后四天,巡游车辆数值与第一天相差较大,数值较小,为了节约临时征用停车位的成本且尽可能地满足第一天的需求,选择18点——20点时间段的数值,即征用245个停车位。
5 结论
本文根据某小镇知名景区的车流量信息数据,通过K-means聚类算法将一天划分为六个时间段,并求得不同时间段四个方向的直行和转弯的车流量;根据韦伯斯特理论建立交通信号灯的配时优化模型,通过粒子群优化算法求得经中路与纬中路交叉口的信号灯周期总时长设置为137s较为合适,其中方向1、2、3、4四个相位的绿灯时间分别设置为27s、47s、50s和35s较为合适;根据五一黄金周期间数据,给出了景区游览游客车辆的判别标准,计算出五一黄金周期间第一天需临时征用411个停车位,后四天需临时征用245个停车位才能满足需求。
参考文献
[1]问题背景和实验数据来源:https://www.mcm.edu.cn/html_cn/node/a0c1fb5c31d43551f08cd8ad16870444.html.
[2]韩雅雯. kmeans聚类算法的改进及其在信息检索系统中的应用[J]. 云南大学, 2016.
[3]李然, 郭谨玮, 黄晓延, 等. 基于多目标粒子群算法的智慧城市信号灯配时优化控制[J]. 中国汽车, 2023(3):41-46.
[4]唐高阳. 单交叉路口交通优化配时控制研究[D]. 东北大学2024.9.8
[5]靳敏, 康乐, 郁宇. 交通信号灯配时优化控制理论研究. 黑龙江工程学院学报(自然科学版)1期:6-9.







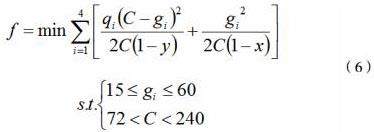


 京公网安备 11011302003690号
京公网安备 11011302003690号


