打开文本图片集

传统的复习课的教学方式为梳理知识内容，构建知识网络，通过例题回顾已学知识，通过练习进一步巩固，以求学生在此过程中夯实基础、提升能力。但这样的教学模式很容易固化学生的思维，形成一种为了复习而复习，仅通过做题复习的僵化模式，不利于发挥学生的主体作用，学生的课堂参与度不高，难以使学生在积极参与学习活动的过程中不断得到发展。在实际教学中，笔者把尺规作图引入特殊四边形复习课，让学生在课堂学习中主动参与观察、实验、猜想、证明等过程，提高学生的课堂参与度，以达到更好的复习效果。下面就本节课谈一谈自己的一点思考。

一、提出问题，引发思考

【探究活动一】

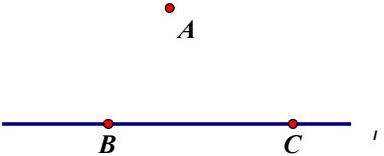
如图，点A在直线l外，点B、点C在直线l上．

在l外求作一点D，使得以A、B、C、D为顶点的四边形是平行四边形并简要说明理由（要求：用直尺和圆规，尽可能运用不同方法作出形状大小不同的平行四边形）；

1．规划方案，参与实践

（教师）：符合要求的点D可能在什么位置？

（学生思考后）：点D有三个可能的位置，并指出大致位置。

（教师）：你能用直尺和圆规确定点D的位置吗？

（学生）：动手操作。

本环节通过学生的思考与交流，是学生能够全面分析，发现点D的位置不止一处，从而使学生养成全面分析问题的思想意识和数学能力，在分析问题的过程中逐步提高合情推理的能力，再利用尺规作图，动手操作，让全体学生都能积极参与课堂研究，通过作图这一数学实践，体会图形的生成过程，激发学生的学习兴趣，为后面的学习做好铺垫。

2．推陈出新，归纳方法

（教师）：刚才同学们都作出了符合要求的点D，能运用不同方法作出符合题目要求的平行四边形吗？

（学生）：分组讨论后，寻找不同方法，并按要求作图。

（教师）：你能谈一谈，你是如何想到你所采用的方法的？

（学生）：以AB、BC为邻边；

以AC、BC为邻边；

以BC为一条对角线；

以AC为一条对角线；

……

本环节通过学生的讨论，发现可以运用不同的方法确定符合要求的点D，进而构造相应的平行四边形，在分析讨论和动手操作的过程中，从不同的角度研究图形的生成过程，使学生能够在获得间接经验的同时，也能有机会获得直接经验，对平行四边形的性质与判定方法有了进一步的认识，更加注重学生的主动发现，而非被动接受，在运用尺规作图的过程中，发现可以采取的手段是不唯一的，从而获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，并且能比较全面的回顾尺规作图的各种基本方法，如作线段垂直平分线，作一个角等于已知角，等等，对学生的操作能力的培养有较大帮助。

3．反思总结，回归目标

（教师）：根据同学们刚才作图的过程，你能简单说明所做图形正确性的依据吗？

（学生）：思考、讨论，得出结论

两组对边分别平行的四边形叫做平行四边形；

两组对边分别相等的四边形是平行四边形；

一组对边平行且相等的四边形是平行四边形；

对角线互相平分的四边形是平行四边形。

本环节通过学生对之前作图过程及结论的讨论、分析，能够非常直观的发现，作图的依据就是平行四边形的判定方法，从而呼应课题，完成本节课的教学目标，在整个学习过程让学生有一种身临其境的感受，自然而然的引发学生的主动思考，充分发挥学生的主体作用，激发学生的学习兴趣。

二、借助经验，主动探索

【探究活动二】

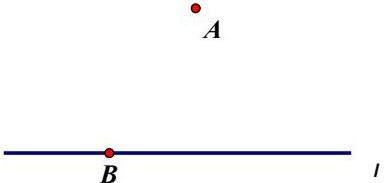
如图，点A在直线l外，点B在直线l上．

在l上求作一点C，在l外求作一点D，使得以A、B、C、D为顶点的四边形是菱形并简要说明理由；（用直尺和圆规，尽可能运用不同方法作出形状大小不同的菱形）

有的学生在思考，有的学生已经动手作图，

（教师）：同学们在动手作图前，可以先预先规划，我要作的图形有什么特征？我可以采用什么方法达到其特征？有哪些不同的方法可以使用？大家可以借助前面的活动经验，结合你对菱形的认识进行讨论。

（学生）：分组讨论后回答

菱形是四条边相等的四边形；

菱形是有一组邻边相等的平行四边形；

菱形是对角线互相垂直的平行四边形。

（教师）：你能否进一步规划具体的可操作方案？

（学生）：可以在直线l上先确定点C，使BC=AB，然后运用探究活动一的方法确定点D，

可以在直线l上先确定点C，使AC=AB，然后运用探究活动一的方法确定点D，

可以先通过作AB的垂直平分线，使之与直线l相交于点C，然后再点D，

学生讨论交流后，动手操作，完成本活动

（教师）：根据同学们刚才作图的过程，你能简单说明所做图形正确性的依据吗？

（学生）：思考、讨论，得出结论

一组邻边相等的平行四边形叫做菱形；

四条边相等的四边形是菱形；

对角线互相垂直的平行四边形是菱形。

本环节活动中，学生因为已经积累了比较多的经验，有了比较明确的研究方向，故而能够更加大胆的参与讨论和交流，做到分解任务目标，逐渐递进研究。在活动过程中，学生显得更加自信从容，无论思考、讨论、交流、总结，都显得更加有条理，课堂参与度有了明显的提高。如果把活动一称为本节课知识的“生长点”，那么，活动二就可以看作知识的“延伸点”，在活动过程中，除了能培养学生主动学习的积极性，直接经历图形的生成过程，体会菱形的特征、性质和判定方法，还能使学生通过问题中条件的变化，理解了图形之间的关联，在注重知识结构和体系的形成过程中，提升了学生思考-交流-操作-总结的基本素养，也进一步提升了学生全面分析问题良好习惯，以及在运动变化中探索图形之间关联的意识和能力。

三、举一反三，提炼升华

【探究活动三】

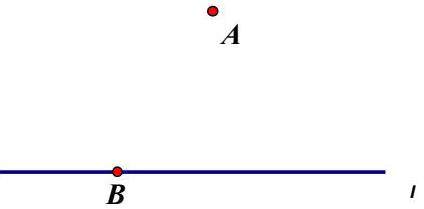
如图，点A在直线l外，点B在直线l上．

在l上求作一点C，在l外求作一点D，使得以A、B、C、D为顶点的四边形是矩形并简要说明理由（用直尺和圆规，尽可能运用不同方法作出形状大小不同的矩形）；

本环节难度稍大，教师在鼓励学生独立思考的同时，可以给予适当启发。

（教师）：我们要确定的有两个点，即点C，点D，借助之前积累的经验，我们要逐一确定，大家觉得应该先确定那一个点？

（学生）：先确定点C。

（教师）：我们还需要弄清楚，矩形有别于平行四边形的主要特征有哪些？

（学生）：思考或讨论后回答

有一个角是直角；

四个角都是直角；

对角线相等。

（教师）：根据前面的两个活动，相信大家可以解决这个问题了。

（学生）：分组交流后，纷纷提出解决问题的方案

在直线l上先确定点C，使∠BAC=90°，然后确定点D，从而构造矩形；

作AC⊥直线l，垂足为点C，然后确定点D，从而构造矩形；

作线段AB的中点O，以点O为圆心，OB为半径作圆，与直线l相较于点C，然后确定点D，从而构造矩形；

……

学生完成作图后，简单说明所做图形正确性的依据

有一个角是直角的平行四边形叫做矩形；

三个角是直角的四边形是矩形；

对角线相等的平行四边形是矩形。

通过本环节活动，学生进一步经历观察、猜想、实验、证明、等实践活动，积累数学活动经验，把已有的间接经验和在活动中获得的直接经验有机结合起来，并在对图形的抽象、分类、位置确定等过程中，积累图形与几何的知识与技能。在活动过程中，锻炼学生综合分析能力，培养类比迁移的研究方法，提高举一反三的应用意识，同时，进一步理解图形的生成过程，熟悉特殊四边形之间的关联，有助于学生理解掌握四边形的特征、性质与判定方法，也锻炼了学生尺规作图的能力，通过作图，梳理四边形的相关知识结构，让学生更加深刻的理解四边形之间的内在联系。

本节课把尺规作图引入四边形复习课，目的是让学生把思考分析与动手操作有机结合起来，避免学生在课堂上 “随大流”、“装模作样”等，让学生能够真实学习，有效复习。立足学生实际，分解复习目标，由易到难，由简入繁，层层递进，把学生的直接经验与间接经验糅合在一起，既能促进学生学习的主动性，通过延长思维链，又能促进学生知识的再生长，通过理论联系实际，动脑与动手相结合，培养兴趣、发展能力、促进学科素养的提升。

姓名：秦卫宏；出生年份：1967年；性别：男；民族：汉；籍贯：南京

职称：中学一级；学历：本科；研究方向：初中几何课堂教学微小专题研究

单位：南京市第十二初级中学