打开文本图片集

摘要：文章基于核心素养的高中数学思维+的视角，结合高中数学教材中的章节内容“函数的极值与导数"展开对组织引导学生进行“说数学”的数学高效课堂构建方法的探究，以期找出一条案例分析路径，为数学高效课堂教学提供思路.

关键词： “说数学”; 高效课堂; 路径

一、问题的提出

教师如何才能成为真正意义上的组织者，引导者和合作者呢？在教学中让学生在课堂上多“说”一些，学生在“说”的过程中，暴露其思维过程，教师才能有针对性组织学生经历“做数学”的过程、提供给学生更合情合理的问题情境引导学生组织，围绕问题的核心进行教学。笔者以北师大版（2019版）《数学》（选择性必修第二册）第二章第2.6.2节“函数的极值”为例，探索思维+课堂“说数学”教学，以飨读者。

二、课例的教学片段

2.1环节一：创设问题情境，唤起学生基本活动经验，生成研究对象

问题1：观察图5.3-9，我们发现当时，高台跳水运动员距水面的高度最大．那么函数在此点的导数是多少呢？此点附近的图象有什么特点（单调性）？相应地导数的正负性有什么变换规律？

生1：当时，函数单调递增，；当时，函数单调递减，．

师：这就是说，在附近，函数值先增后减．当在附近变化时，随着增大而增大时，先正后负，且连续变化，于是有．

问题2：探究教材80页：如图2-16，函数在x1、x2、x3、x4、x5等点的函数值与这些点附近的函数值有什么关系？在这些点的导数值是多少？在这些点附近，的导数的正负性有什么规律？

生2：可以发现函数在点：c=x1、x3、x5的函数值比它在点附近其他点的函数值都大， 0；而且在点附近的左侧＞0，右侧＜0．

师：归纳定义1：若函数y＝f（x）在点x＝a的函数值f（a）比它在点x＝a附近其他点的函数值都小，f′（a）＝0，而且在点x＝a附近的左侧＞0，右侧＜0，就把x＝a叫做函数y＝f（x）的极大值点，f（a）叫做函数y＝f（x）的极大值．

2.2环节2：合作交流“说数学”，构建新的基本活动经验，提升数学思维

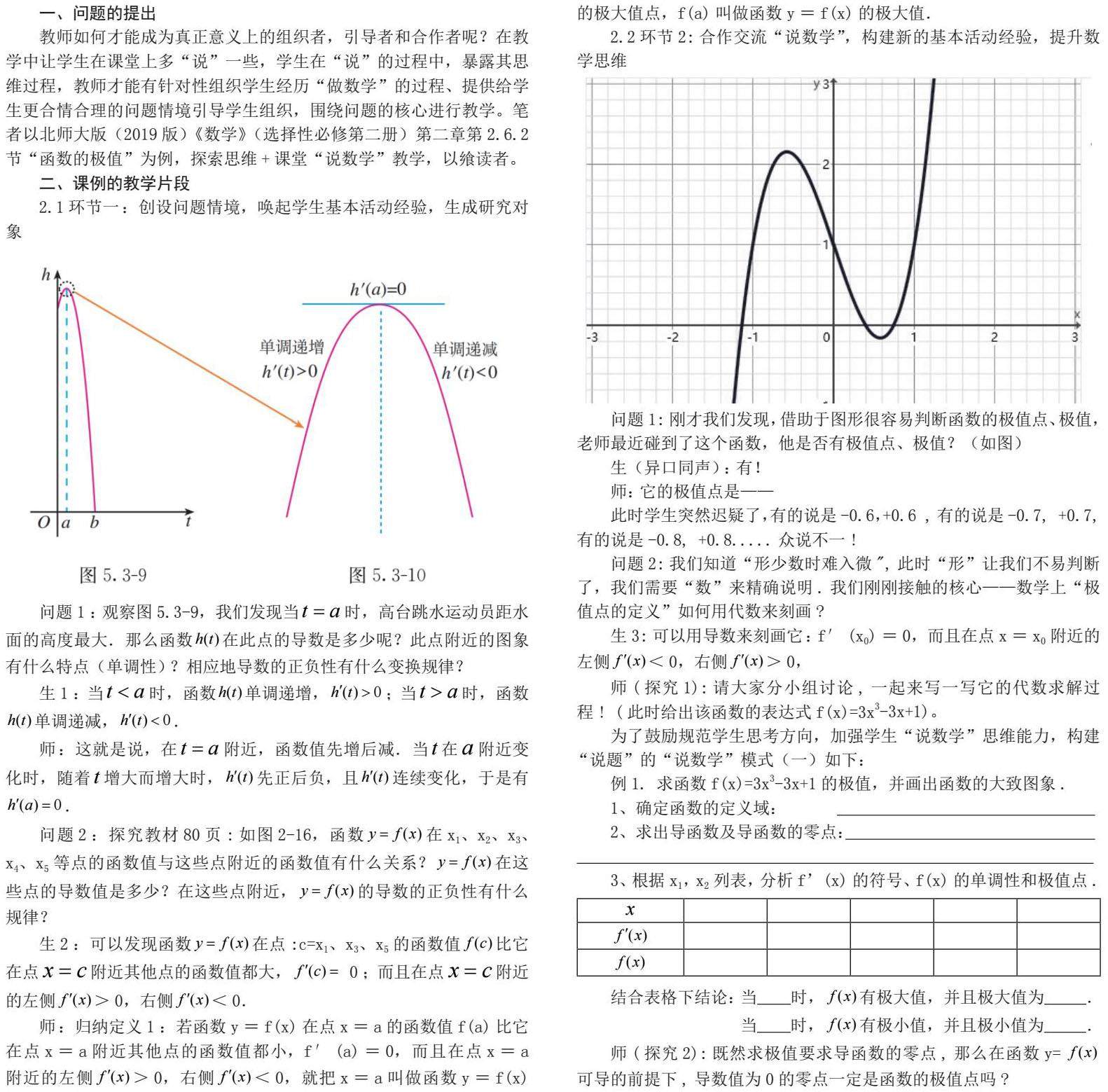
问题1：刚才我们发现，借助于图形很容易判断函数的极值点、极值，老师最近碰到了这个函数，他是否有极值点、极值？（如图）

生（异口同声）：有！

师：它的极值点是——

此时学生突然迟疑了，有的说是-0.6，+0.6 ，有的说是-0.7， +0.7，有的说是-0.8， +0.8.....众说不一！

问题2：我们知道“形少数时难入微"，此时“形”让我们不易判断了，我们需要“数”来精确说明.我们刚刚接触的核心——数学上“极值点的定义”如何用代数来刻画？

生3：可以用导数来刻画它：f′（x0）＝0，而且在点x＝x0附近的左侧＜0，右侧＞0，

师（探究1）：请大家分小组讨论，一起来写一写它的代数求解过程！ （此时给出该函数的表达式f（x）=3x3-3x+1）。

为了鼓励规范学生思考方向，加强学生“说数学”思维能力，构建“说题”的“说数学”模式（一）如下：

例1. 求函数f（x）=3x3-3x+1的极值，并画出函数的大致图象.

1、确定函数的定义域：

2、求出导函数及导函数的零点：

3、根据x1，x2列表，分析f’（x）的符号、f（x）的单调性和极值点.

结合表格下结论：当 时，有极大值，并且极大值为 ．

当 时，有极小值，并且极小值为 ．

师（探究2）：既然求极值要求导函数的零点，那么在函数y=可导的前提下，导数值为0的零点一定是函数的极值点吗？

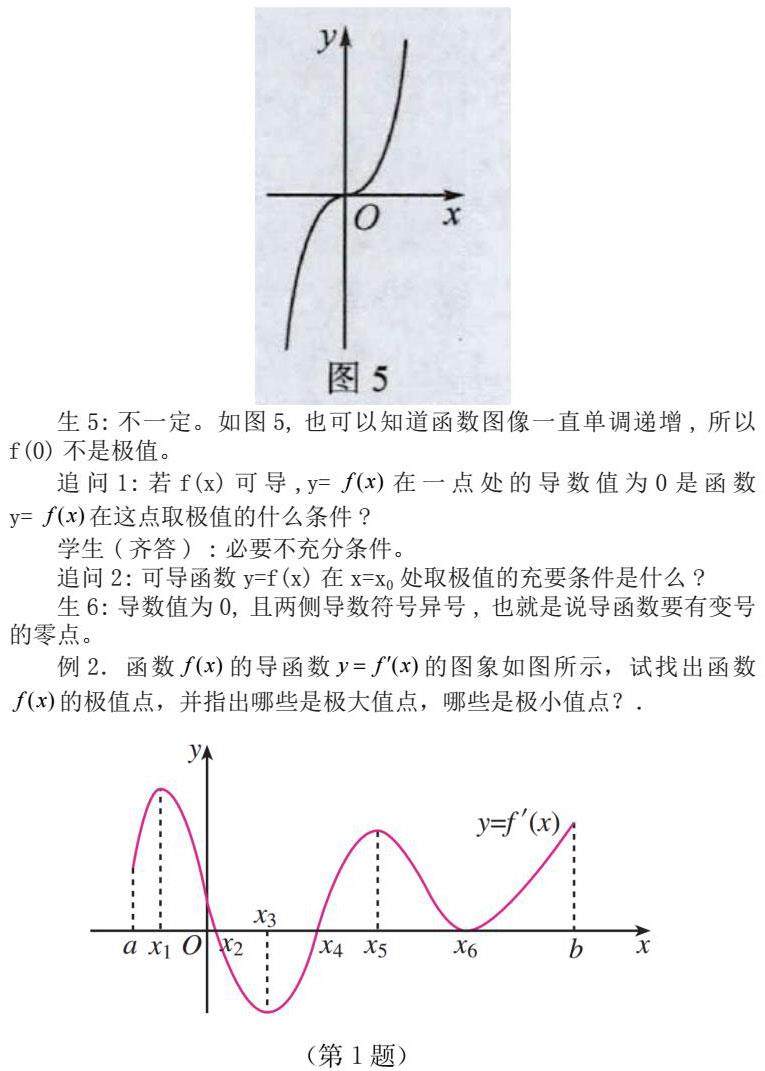
生5：不一定。如图5，也可以知道函数图像一直单调递增，所以f（0）不是极值。

追问1：若f（x）可导，y=在一点处的导数值为0是函数y=在这点取极值的什么条件？

学生（齐答） ：必要不充分条件。

追问2：可导函数y=f（x）在x=x0处取极值的充要条件是什么？

生6：导数值为0，且两侧导数符号异号，也就是说导函数要有变号的零点。

例2．函数的导函数的图象如图所示，试找出函数的极值点，并指出哪些是极大值点，哪些是极小值点？．

搭建辨析思路，构建“说题”的“说数学”模式（二）如下：

1、辨析图象是原函数图还是导函数图：

2、明确原函数图看单调性、导函数图看函数值正负：

抓住极值点的二要素——导数值等于0、左右两侧导数值异号：

三、教学设计说明

3.1设计背景

根据高考的特征，高考评价体系将这三个方面关键能力的发展水平作为主要考内容，以区分学生综合能力水平的高低，引导基础教育对学生综合能力的培养，这对我们的教学改变发出了重要的信号。

3.2以核心素养为导向进行单元设计，构建知识网络

建构大函数单元的意识对函数教学特别重要，设计具体的每单元教学活动、每单元主题活动，让学生在数学课堂上从会“说数学”到敢“说数学”为导向，更加高效与精确实现核心素养的培养目标。

四、总结

在“说数学”课堂中，学生的主体地位和教师的调控地位是交往的基本特点，其凸显的是一种和谐民主而平等的师生关系，是一种你中有我我中有你的整体联系。因此，教师应着重和谐而互动的“说数学”的课堂关系的构建和维系，使交流能在整个学习共同体中顺利进行。

参考文献

［１］林崇德．构建中国化的学生发展核心素养［Ｊ］．北京师范大学学报，2017-06.

［２］王沛钰．高中生数学核心素养的培养需要树立的几点观念［Ｊ］．数学教学教育研究，2017-07