打开文本图片集

摘  要：当前，我校正在开展市级课题《初中数学“学·导·用”教学模式研究》，其出发点是通过课堂模式的变革，更好地培养学生的自主学习能力，最终目的是让学生学以致用，激活数学有效课堂。本文结合近年来的 “学·导·用”课堂教学实践，对其中“运用活学”环节的课堂具体操作糢式进行了大胆尝试，形成“联用”“活用”“巧用”“拓用”等四个方面的策略。

关键词：学·导·用 ；自主；课堂

“学·导·用”教学模式的课堂四个环节包含“目标引学”“前置先学”“释疑导学”和“运用活学”，其中的“运用活学”至关重要。教师通过引导学生自主学习，让学生“运用活学”、学以致用，最后达到激活数学有效课堂的目的，是“学·导·用”教学模式成功运用的结果。以下是笔者在课堂具体操作糢式中进行了大胆尝试形成的一些“运用活学”的具体策略。

一、联用

联用，是指从教材中的例、习题出发，根据问题的特点，充分挖掘知识之间的联系，激活学生头脑中原有的相关知识和经验，从而使学生能够灵活地解决各种相关的问题。

案例1  “联用”人教版课标教材八年级上册“11.1.2 三角形的高、中线与角平分线”教材习题11.2第9题。

原题：如图，∠1=∠2，∠3=∠4，∠A=100°，求x的值.

学生通过自主思考完成此题的解答后，教师首先指出：“此题属于三角形两条内角平分线的夹角问题。”然后提出问题：“你还能找到哪些三角形内角或外角的平分线相交的情形？能画出相应的图形吗？”让学生带着问题去思考、画出图形，并引导学生归纳、总结，最后共得到如下4种不同类型的图形，它们所体现的数学问题分别是：

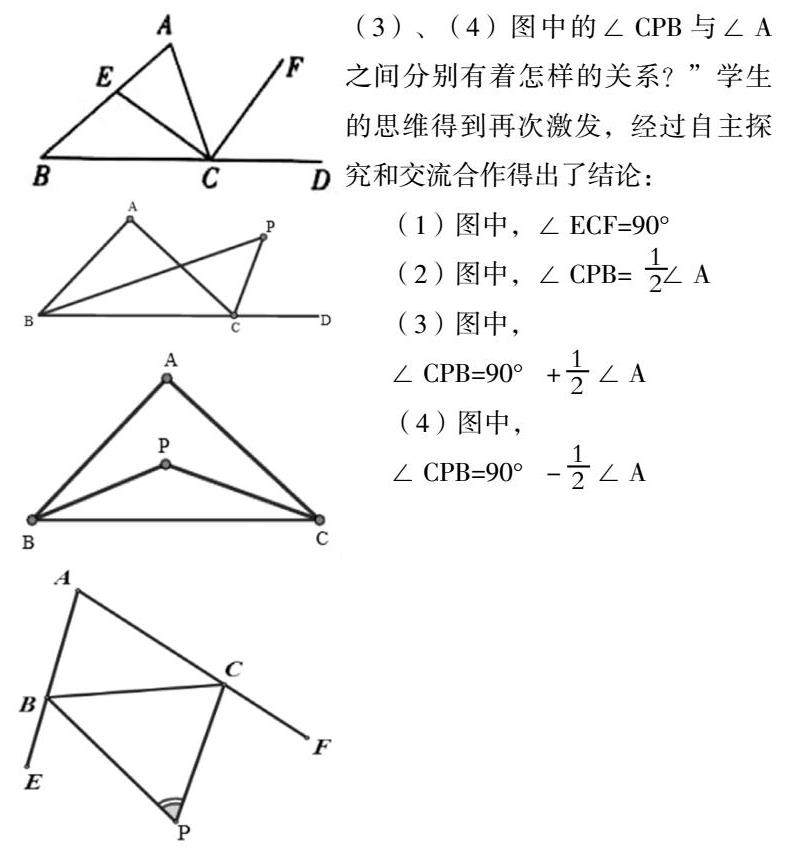
（1）三角形在同一顶点处引出的内角平分线和外角平分线的夹角问题（如图）；

（2）三角形不在同一顶点处引出的内角平分线和外角平分线的夹角问题（如图）；

（3）三角形两条内角平分线的夹角问题（如图）；

（4）三角形两条外角平分线的夹角问题（如图）；

接下来，教师引导学生一边观察图形一边思考，根据图形继续提出问题：“你能求出（1）图中的∠ECF等于多少吗？（2）、（3）、（4）图中的∠CPB与∠A之间分别有着怎样的关系？”学生的思维得到再次激发，经过自主探究和交流合作得出了结论：

这种逐层深入的问题串训练，能打开学生的数学思想之路，有效培养学生的发散思维能力，提高学生的创新意识。

二、活用

活用，是依据教学的实际，对教材中例、习题的条件适当加以改变，以达到拓展学生思维，培养学生建构知识能力的目的。

1.变封闭性问题为开放性问题

初中数学教材中例、习题的条件和答案大多是封闭、唯一的，课堂教学时，可以根据教学内容，变原题条件和答案的封闭性为开放性，以培养学生思维的广阔性。

案例2  “活用”人教版课标教材八年级下册“18.1.2 平行四边形的判定”中的例3。

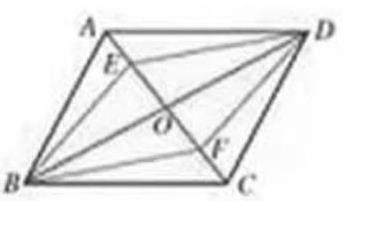
原题：“如图，平行四边形ABCD的对角线AC和BD相交于点O，点E和F在AC上，且AE=CF.求证：四边形BFDE是平行四边形.”改为“在平行四边形ABCD中，对角线AC和BD相交于点O，点E和F在AC上，你能够补充一个条件，使四边形BFDE是平行四边形吗？可以有几种方法？”这种开放性的问题，能够有效激活学生的思维，更好的培养了学生思维的灵活性和创造性。

2.把问题条件“变静为动”

教学中把问题条件“活化”，创设符合课堂需要的数学探究活动情境，不仅能够调动学生的学习热情，并且能激发学生探究的欲望。

案例3  “活用”人教版课标教材八年级上册“15.1分式”。

学习了分式的概念后，可以对教材中的练习题2“下列式子中，哪些是分式？哪些是整式？两类式子的区别是什么？  ，  ，        ，      ，        ，      ，           ，

.”的条件作灵活的改变，创设一个“组分式”的游戏活动：“已知整式1，x，3，4，3b2+5，2a-5，x2-y2，m-n，m+n，x2+2x+1，x2-2x+1，c，3（a-b）.试从这些整式中任意选出2个，用它们组成一个分式（至少写出3个分式），最多可以组成多少个用分式？”通过这样的主动性活动，不仅有效激发了学生的学习兴趣，并且还培养了学生的创造思维能力。

三、巧用

近几年，中考中出现了以框图、图表、新定义概念、数学过程等形式呈现的问题。巧用，是指根据教学内容的特点，立足于学生的实际，巧妙地改变数学问题的呈现方式，以增强学生的阅读理解和运用、处理信息的能力，帮助学生适应不同的命题形式，从而有效地培养学生解决问题的能力。

案例4  “巧用”人教版课标教材八年级下册“18.2.3 正方形”。

教材中，一开始就直接给出正方形的概念和性质：“正方形（ Square）是我们熟悉的几何图形，它的四条边都相等，四个角都是直角。因此，正方形既是矩形，又是菱形。它既有矩形的性质，又有菱形的性质。”

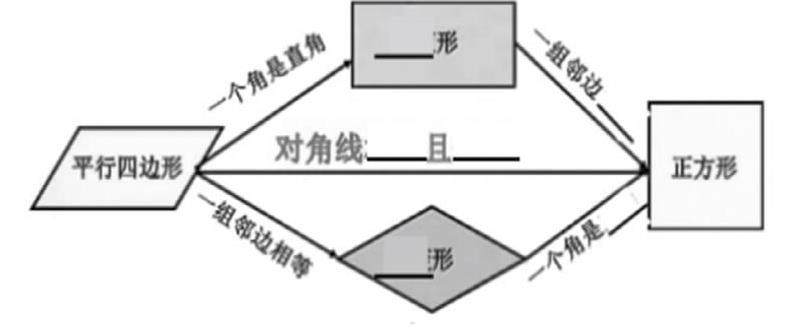
此时，教师首先让学生独立阅读正方形的概念，然后引导学生归纳正方形的性质及正方形与矩形、菱形的区别和联系，接着教师对这个概念和性质进行了“巧用”——以框图的形式呈现有关的问题，并引导学生在框图对应位置填入图形的名称和转化的条件。

通过这种改变数学问题呈现方式的方法，引导学生把抽象难懂的概念转化为思维导图，能提高学生的阅读、理解和处理信息的能力。

四、拓用

拓用，是指对教材中的例、习题进行适当的拓展和延伸，提供更广阔的学习空间和思考空间给学生，以提高学生的学习能力。

案例5  “拓用”人教版课标教材八年级上册“13.3.2 等边三角形”中习题13.3的第12题。

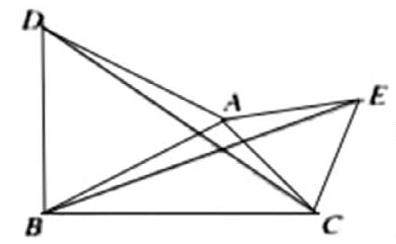
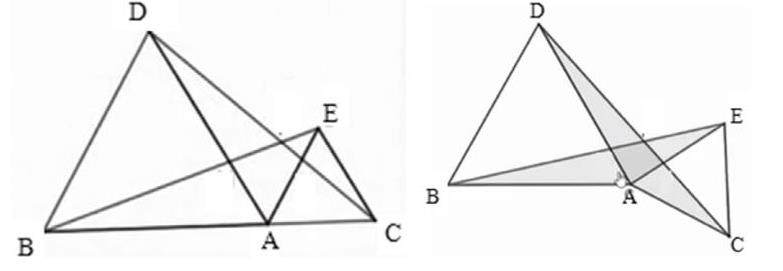
原题：如图，△ABD和△AEC都是等边三角形.求证BE=DC.

当学生完成此题的解答后，教师继续提问：“若将图中的△ABD固定不动，保持△AEC的形状和大小不变，将△AEC绕着点A旋转，得到如下两种情形，这时BE=DC吗？”

这种图形变化中结论的变与不变问题，有效地激活了学生的思维，教学中，教师可以先利用几何画板进行动态演示，让学生边观察图形的变化，边探究、猜想BE与DC的大小关系，并给出证明。

在解答这道拓展题后，教师应引导学生反思整个探究过程，从中发现：虽然图形经过旋转发生了“形”变，但结论仍保持不变，这种“拓用”使学生感受到知识的发生、发展过程，培养了学生的类比猜想和探究推理能力。

如果我们能在数学课堂中运用更多有效的策略，让学生把所学知识“运用活学”、学以致用，那么我们的课堂必定会越来越精彩，会有更多更好的愉快课堂、生活课堂、创造课堂呈现在学生的视野中，我们的数学教学才会提升到一个新的层次。

【参考文献】

[1]何超英.浅谈教材例、习题资源的使用策略[J].中国数学教育.2009（09）

[2]位国权.浅谈初中数学课堂教学中的练习[J].成功（教育）.2013（01）

[3]张超群.做活“释疑导学”构建有效课堂——“学·导·用”教学模式中“释疑导学”的实践与思考[J].黑河教育.2018（10）