摘要：本文针对一种非线性的工作绩效考核模型，分别基于合作博弈夏普利值分配方法以及传统比例分配法对考核结果进行分解，仿真结果表明，与传统比例分配法相比，夏普利值方法对需倾向关注的因素更为敏感，更能贴合模型特征函数的倾向性要求。

关键词：合作博弈 夏普利值 比例分配 边际贡献

1 引言

在一些矩阵型组织中，对工作绩效的考核方式较为特殊，业务部门层面的绩效基本盘由上级组织确定，再根据业务部门所承担的全部工作绩效完成情况进行扣减。绩效考核时结合重要程度进行加权，例如将整体工作完成情况与重要工作的完成情况相乘，来得出最终考核结果。该考核方式下，各工作完成情况存在交互效应，是一个非线性模型，传统的比例分配法难以准确解耦单个工作完成情况与考核结果间的关系，且对重点工作的实际贡献敏感性不足。

本假设下重点工作与其余工作分属于不同群体，最终考核结果由二者共同决定，属于合作博弈，而合作博弈论中的夏普利值方法因其有效性、对称性、线性性以及零贡献者不分配的特点，为多变量收益提供了天然分配框架 [1]。本文根据前述模型假设，探讨如何基于夏普利值方法将业务部门的工作整体绩效考核结果分解至单个工作，并与传统的比例分配法进行了对比。

2. 考核模型的假设

假设业务部门共承担 m 个重点工作和 n 个其他工作，各工作的任务完成情况互相独立。将工作按重要程度分为 4 类，引入重要程度系数Vi ，定义Vi ∈[1，2，3，5]，规定 Vi =5 的工作为重要工作。为突出重点工作的影响，按照模型假设，规定考核结果为整体工作完成率与重点工作任务完成率之积。

一般情况下，完成率高于未完成率，将考核结果进行分解时，主要考虑未完成的工作对考核结果的贡献。因此定义单个工作的未完成率为考核周期内该工作未完成任务的数量占总任务数量的比例，单个工作加权未完成率为其未完成率与重要程度系数之积，总重要程度系数为部门承担的全部工作的重要程度系数之和，重点工作总重要程度系数为部门承担的重点工作的重要程度系数之和。

模型中的各参数定义及变量设定如表1 所示依据模型假设，业务部门承担的工作整体完成率为：

表1 考核模型参数定义及变量设定

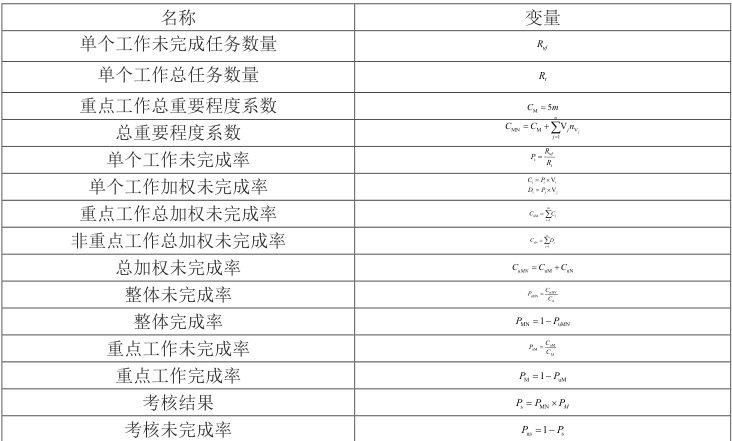
5. 仿真分析

在本模型假设中，对业务部门进行考核时重点工作绩效多次作用，说明本模型中对重点工作有所偏重，因此向下分解时也应向重点工作倾斜。对两种分配方式下单个工作的边际贡献率[3] 进行仿真，取 m=10 ， n=20 ，Ci 在 0-5 取值， D_j^† 分别在 0-1（v 个），0-2（ w 个），0-3（ n-V-W 个）间取值， v 和 w 随机生成，结果如图1 所示。

图 1 边际贡献率对比图

从图中可看出，夏普利值法更偏重于重点工作的贡献值。取 m=20 ， n=120 ，分别绘制两种分配方式的条形图和散点图，如图2 和图3 所示：

图 2 一般情况分配值条形图对比

图 3 一般情况分配值散点图对比

从图中可看出，与传统比例分配法相比，对于非线性模型，夏普利值分配法更能体现倾向性和差异性，对考核模型倾向关注的重点工作分配更为充足，更适合用于本模型中的分配情况。

6. 结束语

本文基于假设的工作绩效考核模型，提出了一种基于合作博弈论夏普利值的工作绩效分解方法，将夏普利值分配法与传统比例分配方式进行了对比，并对一般情况下的表现进行了仿真，可看出在本模型中夏普利值分配法相对于比例分配法更能体现模型对重点工作的倾向性与差异性。

参考文献

]Osborne， M. J. & Rubinstein， A. （1994）. A course in game theory [M]. MIT Press.

[2]Shapley， L. S.， & Shubik， M. （1969）. Values of large games I： A limit theorem. Internationa Journal of Game Theory， 3（1）， 1-14.

[3] 李明 ， 王强 .《边际贡献理论及其在绩效评价中的应用》[M]. 北京：中国经济出版社 ，2012 年 .

作者简介：樊钦，大学本科，工程师，研究方向：项目管理。