摘要：随着教育评价体系的完善，认知诊断作为一种先进的测评方法受到了广泛关注。本文通过引入广义 DINA（G-DINA）模型，研究了高中数学向量问题的认知诊断方法。G-DINA 模型能够深入分析学生解题时的认知过程和能力结构，帮助教师识别学生的知识掌握程度和认知缺陷。通过对向量问题的分析，本文构建了基于 G-DINA 模型的认知诊断框架，并应用于具体测试，探索学生的认知结构。研究表明，G-DINA 模型能有效揭示学生的认知特点，分析薄弱环节，并提出针对性教学建议。本研究为数学教育提供了一种新的认知诊断工具，也为教学改进提供了参考。

关键词：G-DINA 模型，认知诊断，高中数学，向量问题，数学教育

引言：

随着教育理念的更新和教学方法的创新，传统评估方法已无法满足个性化学习的需求。认知诊断逐渐成为教育领域的重要研究方向，其核心是通过分析学生的认知能力和解题过程，精准评估学习状况。传统评估侧重于答题正确率，忽视了解题过程中的认知结构。G-DINA 模型作为一种灵活的认知诊断工具，能够全面分析学生的认知能力。在数学教育中，特别是向量问题的解答过程中，G-DINA 模型能有效揭示学生的认知策略与知识结构，为教学改进提供精准方向。

一、G-DINA 模型的理论背景与应用

G-DINA（Generalized DINA） 模 型 是 基 于 传 统 的 DINA（Deterministic Input，Noisy“And”Gate）模型的扩展和改进，能够对学生在完成特定任务或问题时的认知过程进行细致的分析。DINA 模型本身是通过假设学生对不同知识点或认知元素的掌握状态，进而预测学生在任务中的表现，而 G-DINA 模型则引入了更为复杂的认知元素结构和潜在能力变量，增加了模型的灵活性和适应性。G-DINA 模型能够同时考虑多个认知元素之间的交互作用和潜在能力的影响，适用于对学生的多维认知能力进行综合评估。该模型的核心优势在于能够不仅仅依赖学生的最终答题结果，而是通过分析学生的解题过程，深入挖掘学生的认知状态及其影响因素。

在教育测评中，G-DINA 模型的应用广泛且多样。它不仅可以用于学科知识的评估，还能应用于各类技能的测试，特别是在数学、科学等学科中，能够准确揭示学生在解题过程中的认知缺陷和知识结构。尤其对于像高中数学中向量问题这样的复杂问题，G-DINA 模型通过对学生在解答过程中的策略、错误类型和知识点掌握情况的分析，能够提供更为细致的认知诊断，帮助教师更加清楚地了解学生的学习进度和潜在问题。

二、高中数学向量问题的认知诊断研究设计

本研究通过选取高中数学中的向量问题，结合 G-DINA 模型，进行认知诊断分析。高中数学中的向量问题涉及到多个知识点的融合，包括向量的定义、运算、坐标表示、向量之间的关系等内容。这些问题往往具有较高的抽象性，且解答过程需要一定的逻辑推理能力和计算能力，因此，学生在解答向量问题时可能面临不同层次的认知挑战。

本研究首先构建了一个涵盖高中数学向量知识的认知诊断框架，分析了影响学生解答向量问题的主要认知因素。接着，选择了一系列具有代表性的向量问题作为测试任务，涉及从基础的向量加减法到更为复杂的向量投影、向量的夹角计算等问题。每个问题都设计了若干个子任务，每个子任务对应一个或多个认知元素，目的是通过学生对这些任务的解答情况，深入分析学生在向量问题中的知识掌握情况。

通过 G-DINA 模型，研究团队对学生在向量问题中的表现进行了全面的诊断，揭示了学生在认知层面的优势和不足。具体来说，模型通过分析学生在不同认知元素上的表现，帮助识别学生在向量知识的不同方面存在的认知漏洞，进一步了解学生解题过程中可能出现的错误类型和思维偏差。

三、实验数据分析与结果

为了验证 G-DINA 模型在高中数学向量问题认知诊断中的应用效果，本研究使用了一组来自某高中数学课堂的实际测试数据。测试对象为该校高二年级的学生，共计 150 人。测试内容包括多个具有不同难度的向量问题，旨在全面考察学生在向量知识领域的认知水平。

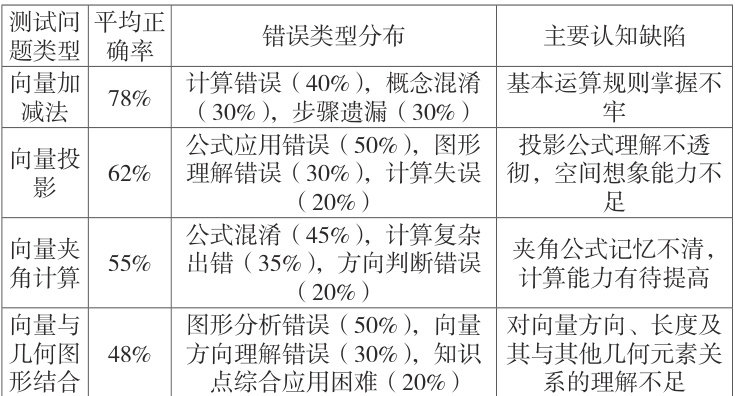
通过对数据的处理与分析，研究发现，G-DINA 模型能够有效地揭示出学生在向量问题中的认知模式与能力结构。首先，在基础向量知识的掌握方面，大部分学生能够较好地理解向量的基本运算和几何意义，但在向量的应用和综合性问题上，存在明显的认知偏差和漏洞。尤其在向量与几何图形结合的问题上，学生的答题正确率较低，且错误类型较为集中，主要表现为对向量方向、长度及其与其他几何元素关系的理解不足。

其次，模型分析显示，学生在解答向量问题时的思维模式具有较强的个性差异。一部分学生能够灵活运用向量的性质和运算规则，解答较为复杂的问题；而另一部分学生则在面对稍微复杂的题目时，出现了知识点回忆不足、计算步骤遗漏等问题。通过认知诊断结果，教师可以更加明确地识别学生在学习向量时的认知漏洞，从而制定更具针对性的教学方案。

四、教学策略与实践建议

基于 G-DINA 模型的认知诊断结果，本文提出了以下几项教学策略和实践建议：首先，教师应针对学生在向量问题中暴露出的薄弱环节，进行有针对性的复习和强化训练。例如，对于学生在向量与几何图形结合问题中的困难，教师可以通过具体的案例分析和形象化教学，帮助学生加深对向量性质和几何意义的理解。通过示范具体的计算步骤和图形分析，教师可以引导学生从直观角度理解向量的应用，提高他们的空间思维能力。其次，教师可以根据 G-DINA 模型提供的认知诊断数据，进行差异化教学，针对不同层次的学生设计不同难度的练习题，帮助学生逐步突破认知瓶颈。通过为学生提供适应其认知发展水平的题目，教师能够有效提高学生的解题能力，避免过于简单或过于困难的题目导致学生的学习挫败感。最后，教师应鼓励学生通过自主学习和小组合作，探索向量问题中的多种解法，培养学生的创新思维和解题策略。通过合作学习，学生可以互相分享解题经验，互相启发，进而提高他们对向量问题的理解深度和广度。教师还可以利用现代技术手段，提供线上学习资源和互动平台，帮助学生在课外自主学习和复习时进行自我检测和反馈。

五、结论

本文基于 G-DINA 模型，针对高中数学中的向量问题进行了认知诊断研究。研究表明，G-DINA 模型能够有效揭示学生在向量问题中的认知特点，分析学生的知识掌握情况和认知缺陷，从而为教学提供了有力的支持。通过对学生认知过程的深入分析，教师可以更加精准地进行个性化教学，帮助学生更好地理解和掌握向量知识。未来，随着教育数据分析技术的不断进步，认知诊断方法将在更多学科和领域中得到应用，推动教育评价的科学化和个性化发展。

参考文献：

[1] 厚亚荣 .STEAM 教育理念下高中数学教学改革实践研究 [J]. 考试周刊 ，2024，（45）：64-67.

[2] 包洪乾 . 基于精准教学分析的高中数学教学实践策略 [J]. 数学学习与研究 ，2024，（20）：26-28.

[3] 董晓丽 . 基于核心素养的高中数学单元教学设计研究 [D]. 西南大学 ，2024.DOI：10.27684/d.cnki.gxndx.2024.000912.