摘要：本研究依托DOPBL 模式，将高中数学三角函数与物理简谐振动进行跨学科融合，构建问题驱动的教学情境，设计分组探究、实验数据建模与函数拟合等实践活动。通过项目化学习，学生不仅掌握了三角函数与简谐振动的知识联系，还在数学抽象、科学探究与合作创新等核心素养方面得到显著提升，为跨学科教学提供了可推广的路径。

关键词：核心素养；DOPBL 模式；三角函数；简谐振动；跨学科教学

一、跨学科实践的教学设计思路

（一）学科知识目标与核心素养目标的融合

在核心素养导向下，跨学科教学更加注重学生综合运用知识解决问题的能力，而非单纯的知识掌握。在本研究中，数学三角函数的教学目标是学生能够掌握函数基本性质、图像和解析表达能力，而物理简谐振动部分的目标是学生理解位移、速度、加速度随时间的变化规律和实验验证，两者在时间函数表达和周期性特征方面有天然的契合点。因此在教学设计过程中不仅要实现知识目标，还要在学科知识学习过程中培养学生数学抽象、科学探究、逻辑推理、实践创新等核心素养，使得学科知识学习与综合能力培养相辅相成。

（二）问题驱动情境的创设与项目任务的提出

DOPBL 模式的关键在于通过问题驱动学生探究兴趣，教学过程中可以围绕“如何用数学方法来描述物理中的简谐振动”这一主线问题设计项目任务。例如引导学生观察摆球、弹簧振子、声波振动现象，提出“位移如何随着时间变化”、“周期和频率如何确定”、“如何用函数图像来描述运动规律”等问题。这些问题既有真实性也有挑战性，能让学生处于跨学科探究的主动位置，进而调动自己已有的数学与物理知识进行整合与应用，形成从问题到项目的逻辑递进。

（三）跨学科知识链条的构建：从三角函数到简谐振动

跨学科实践设计要重视知识间的联系，三角函数的正弦，余弦函数具备周期性和对称性，正好可用来描绘简谐振动时位移随时间的改变情况。在教学里，可引领学生先从三角函数基本图像着手，体会它的周期，相位和振幅所代表的物理含义。再逐步过渡到简谐振动公式的x=Asin(ωt+φ) 推导与应用。通过这样的链条式知识连接，学生就能清楚知晓数学函数不是抽象符号，而是表达物理现象的语言，从而达成跨学科知识的自然融合。

（四）实践活动流程设计与学习方式的多样化

DOPBL 模式下实践活动流程要遵循“驱动——组织——问题解决”，教学流程分为四阶段：先生活化或实验情境驱动学生发现问题，再组织学生分组合作，确定任务分工并设计探究方案。然后学生实验操作、数据采集、数学建模解决问题，利用函数拟合等方法分析实验数据并作图，最后组织成果展示交流，引导学生多角度反思评价。学习方式既包含小组合作学习，也包含个体探究和课堂讨论，教师起组织者、引导者作用，多样学习方式让学生加深对数学、物理知识理解，又能在合作探究中培养沟通、批判、创新等能力，达成跨学科实践综合育人。

二、教学实施与案例分析

（一）教学组织与分组合作模式

在实际操作中，采取小组合作学习的方式，把班级学生按照学业程度以及兴趣的差别分成小组，每组安排组长，实验记录员，数据分析员，汇报员等角色。让每个同学的任务分配清晰明确，教师运用 DOPBL 模式当中的“组织”部分，引导学生知晓项目任务以及研究步骤，并给予实验器材和参考资料。在这样的组织形式之下，学生们可以在合作当中发挥自己的优势，既能增进团队合作的意识，又能锻炼各自探究的责任感。

（二）三角函数知识在简谐振动实验探究中的应用

在实验探究中，教师引导学生把数学三角函数知识迁移到物理简谐振动的描述上，简谐振动的位移函数可以表示成： x(t)=Asin(ωt+φ) 。其中，其中 A 是振幅，ω 是角频率， Φ 是初相位，学生通过对比数学中正弦函数的性质，可以理解周期 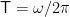与频率 f=1/T 的关系。比如如果一个振动系统的周期测量得到是 T=2s ，那么角频率就是 ω=π rad/s，在此基础上，学生根据实验现象（摆球或者弹簧振子）描绘出位移随时间变化的曲线，再与数学三角函数图像对应起来，加深对物理现象函数化的认识。

（三）实验数据采集、建模与函数表达

在实验实施中，学生通过传感器或视频分析软件采集振子在不同时间下的位移数据。例如，某实验组得到的数据为：

学 生 可 利 用 三 角 函 数 进 行 拟 合，发 现 数 据 基 本 符 合 模型： x(t)≈5sin(πt)

拟合结果显示振幅约 5cm，周期为 2s，与观察高度一致。这一过程不仅要求学生掌握函数建模方法，而且让学生体会参数 A，ω， Φ 的意义，做到数学和物理的融合。

（四）学习成果展示、交流与评价

实验结束之后，每个小组要上交探究报告并做课堂展示，报告中包含实验设计，数据处理，函数模型拟合和误差分析等内容，教师和学生一同展开评价，评价维度涉及“问题解决能力”，“跨学科知识应用”，“合作过程表现”以及“成果创新性”。例如，某小组提出利用余弦函数 x(t)=Acos(ωt+φ) 也可描述简谐振动，并通过相位平移公式验证了正弦与余弦模型的等价性，显示出较强的数理迁移能力。在交流过程中，不同小组的方案互为补充，促进了学习成果的共享与提升。

（五）简谐振动求导方法题目引入

为了进一步加深学生对简谐振动与数学知识联系的理解，引入一道高中物理上简谐振动求导方法的题目：已知一简谐振动的位移函数为 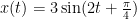，求该简谐振动的速度函数 v(t) 和加速度函数 a(t) 。解题步骤如下：

求速度函数：根据位移函数求导得到速度函数，即 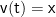’ (t) 对于 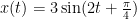，利用复合函数求导法则，设 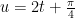，则 x=3sinu 。先对先对 sinu 关于 u 求导得 cosu，再对 u 关于 t 求导得 2，根据复合函数求导公式 (f(g(t)))^′=f^′(g(t)⋅g^′(t) 可得， 。

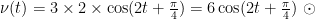求加速度函数：由速度函数求导得到加速度函数， a(t)=v^′ ’(t)，对于 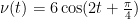，同样利用复合函数求导法则，设 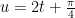，则则v=6cosu 先 对 cos u 关 于 u 求 导 得 -sinu，再 对 u 关 于 t 求 导 得 2，所以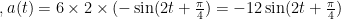

通过这道题目，学生能够更深入地理解简谐振动中位移、速度和加速度之间的关系，以及数学求导在物理中的应用，进一步强化跨学科知识的融合。

结论：

跨学科实践证明，DOPBL 能促进数学物理结合，学生既学知又增慧，加强数据处理及合作才能改进教学效果。

参考文献：

[1] 高会平. 数学向量与三角函数知识在高中物理中的应用例析[J].教学考试 ( 高考物理 ),2022,(4)

[2] 陈春芳 .“函数 y= Asin（ω x+ϕΦ ）的图象”教学设计 [J]. 江苏教育 ,2020,(59):28-32.