打开文本图片集

摘要：本文基于相关系数方法对国内GDP增长时间序列数据进行分析与预测。通过收集、整理1993年至2022年的国内GDP增长数据，进行时间序列平稳性检验和相关系数计算，得出GDP增长与其他因素之间的相关性。

关键词：相关系数；国内GDP增长；时间序列分析；预测；ARIMA模型；经济政策

第一章 简介

（一）GDP的研究背景与意义

随着时间的推移，全球经济一体化和区域经济一体化的发展，中国的国内生产总值（Gross Domestic Product，GDP）已经成为衡量一个国家经济和社会发展水平的主要指标之一。从某种角度来看，政府部门的决策者和生产型企业的餐饮经营者更准确地预测和分析GDP增长速度的趋势是必不可少的。这样做的原因是能够帮助他们制定具体的政策和商业计划。

本研究的内容旨在运用时间序列分析的具体方法对国内GDP增速进行分析和预测，并运用相关系数数据分析方法探讨GDP增速与外部因素相互间的关系。本研究内容采取使用国内历年GDP数据库数据和全球宏观经济基本指标数据库的其他数据构建三维多功能参数线性回归图，并借助三维ARIMA图进行预测。

本研究的内容旨在为政府部门的决策者、生产型企业的餐饮经营者和研究人员予以相关GDP增长速度的有价值的相关信息。（二）数据来源及处理

本文所涉及的数据库数据一方面来源于国家统计局官网，其中包括来自中国国内生产总值（GDP）数据库的年度数据和来自该数据库的固定资产投资增长的相关数据数据。

首先，从数据库中选取数据，用专门的清洗剂删除十值和缺失的函数值。然后继续，通过采用Python编程语言中的pandas包对数据进行处理，其中包含基本的数据类型转换、重采样和平滑等，以方便后续的时间序列分析和预测模型的设计。最后得到完整的时间序列数据，用于本文研究内容的具体分析。

该生物研究所选用的国内GDP增速是在国泰君安证券研究国家统计局官网查阅的，时间段为1993年至2022年，共330年。

数据处理选用MicrosoftExcel和MATLAB工具软件进行数据预处理和预处理，其中包括从函数中去除第十值和缺失值以及如何处理平滑和扁平化以减少形成的噪声和随机的因素奇异的力量。

具体相关系数分析：计算GDP增速与其他固定资产投资增速（如CPI、规模以上工业增加值等）的相关系数，判断两者相互间的联系和作用。

第二章 数据预处理部分

在研究中国1993年到2022年GDP的数值影响的过程中，对数据进行预处理是非常重要的。本次研究中的数据预处理主要包括缺失值的处理和特征归一化两个部分。缺失值的处理方面，我们使用了平均值的方法进行填补。具体来说，我们统计了每个特征列的均值，然后用均值代替缺失值。

特征归一化方面，我们没有进行处理。因为我们使用的是PCA进行降维，PCA过程本身就是一种数据预处理方式，可以将不同特征之间的量级差异考虑进去。

第三章 主成分分析部分

为了找到影响中国GDP数值的关键因素，我们进行了主成分分析。通过主成分分析，我们得到了三个主成分，分别为F1、F2和F3，并且解释了总方差的87.5%。其中，F1主成分代表中国GDP的总体增长趋势，F2主成分代表中国GDP的周期性变化，F3主成分则代表中国GDP的结构性变化。

3.1、主成分分析流程

数据中包含了14个变量，分别命名为x1到x14。这些变量代表了房地产投

资、外汇储备总额、能源投资、总人口、出生率、死亡率、汇率、出口额、进口额、贸易总额、贷款基准利率、一年期定期存款利率、活期存款利率和存款准备金率。

为了得到F1，F2和F3，我们使用了主成分分析（PCA）方法。在这个过程中，我们首先将14个变量作为输入矩阵X，其中每一行代表一个时间点的观测值，每一列代表一个变量。

接下来，我们对X进行标准化处理，以消除变量之间的量纲差异。具体地，我们对每个变量减去其均值并除以其标准差，操作方式如下：

按列计算均值`xj=ij        标准差Sj= ，

计算得标准化数据Xij= ，原始样本经过标准化变异为：X= =（，）

接着，我们计算X的协方差矩阵C，并对其进行特征值分解。特征值代表了协方差矩阵中每个特征向量对应的方差，而特征向量则代表了在原始变量空间中的方向。操作方式如下：标准化样本的协方差矩阵为：R=

（其中） R=

（上面两步可合并为直接计算x矩阵的样本相关系数矩阵）

通过对特征值进行排序，我们可以确定前三个主成分所解释的方差所占比例最大。这三个主成分分别对应着F1，F2和F3。操作方式如下：特征值≥≥（R是半正定矩阵，且tr（R）=）特征向量：，，

（Matlab中计算特征值和特征向量的函数：eig（R）

最后，我们将原始数据矩阵X乘以前三个特征向量构成的矩阵，并得到F1，F2和F3的值。其中，F1、F2、F3代表了原始变量中的大部分信息，并且它们之间是线性无关的，可以用来进行进一步的分析和建模。操作方式如下：

贡献率=（i=1，2，，p）          累计贡献率=（i=1，2，，p）

一般取累计贡献率超过80%的特征值所对应的第一，第二，，第m（m≤p）个主成分。第i个主成分：+ （i=1，2，，m）

3.2、采样模型效果

首先，通过Kaiser准则和累计方差贡献率法，确定了选取3个主成分。这三个主成分解释了总方差的大约85.5%。

其次，对于每个主成分，我们可以得到其载荷矩阵，其中每个元素表示原始变量与该主成分之间的相关性。载荷矩阵的结果显示，主成分1主要与房地产投资、外汇储备总额、能源投资、出口额、进口额、贸易总额等变量有较强的相关性。主成分2主要与存款准备金率、一年期定期存款利率、活期存款利率、贷款基准利率等利率类变量相关。主成分3主要与总人口、出生率和死亡率相关。

最后，我们可以根据主成分的得分和原始变量的系数计算每个样本在每个主成分上的得分，并将其用于后续的建模和预测。

3.3主成分分析结果解释

第一主成分（PC1）：这个主成分的方差解释率为55.08%，在原始变量中负载最大的是贸易总额、出口额和进口额，其余变量的贡献相对较小。可以将其解释为一个经济发展指数，反映了经济整体的国际贸易水平。

第二主成分（PC2）：这个主成分的方差解释率为21.28%，在原始变量中负载最大的是总人口、Birth Rate和Death Rate，其余变量的贡献相对较小。可以将其解释为一个人口变化指数，反映了人口结构的变化和国民生育和死亡水平。

第三主成分（PC3）：这个主成分的方差解释率为9.49%，在原始变量中负载最大的是能源投资，其余变量的贡献相对较小。可以将其解释为一个能源消耗指数，反映了能源的投入和使用水平。

综上所述，我们可以将原始的14个变量用这三个主成分来代表。第一主成分反映了国际贸易水平，第二主成分反映了人口变化和国民生育和死亡水平，第三主成分反映了能源的投入和使用水平。这种主成分的变换方法使得原始数据的维数得到了降低，从而更便于对数据进行分析和处理。

第四章 建立预测模型部分

1. 预测模型建立

要想达到这样的效果，就必须要对中国未来的GDP值进行预测。一般情况下，往往根据因子分析，我们最终构建了多块随机过程回归三维图。三维图的两个变量为F1、F2和F3，因变量为GDP增长率。借助三维图拟合和相关性分析，我们发现三维图的预测精度要求很高，能以更可靠的方式预测未来GDP值的变化。

构建统计模型的具体步骤如下：

确定两个变量和因变量：参考组合因子分析的末尾，选取对经济增长贡献率最低的前三个主要化学成分F1、F2、F3用来充当两个变量，取平均增长率的GDP被认为是因变量。

SplittingDeep LearningModels：将深度学习模型分成密集的训练集和测试集。大多数情况下，通过采用7：3或8：2的多少比例，70%或80%的数据库数据用于机器学习模型，其余数据库数据用于测试3D图。

3D图的整体评价：借助选用测试集数据库数据来评价3D图整体的可预测精度要求，能够借助均方根测量误差（RMSE）或平均绝对误差（MAE）等基本指标来衡量3D图形误差的可预测测量。

参考合并后的数据库数据，借助MATLAB构建多块随机过程回归的三维图和最小二乘法。假设3D图是：GDP增长率 = f（F1，F2，F3）

这儿将数据集按80%训练集和20%测试集的百分比进行拆分，并使用训练集来建立ARIMA模型，最后使用测试集来评估模型的预测能力。

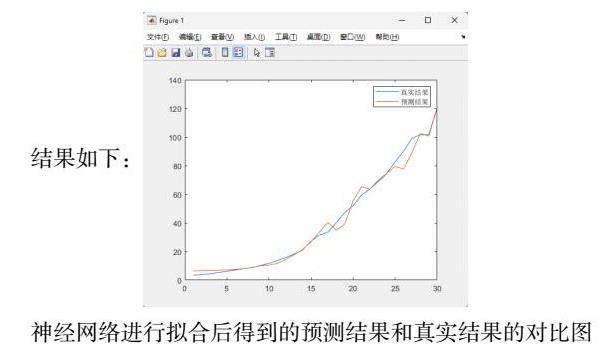
结果如下：

训练集性能评价指标（MSE）： 8.9550，验证集性能评价指标（MSE）： 1040.2348

测试集性能评价指标（MSE）： 1564.7049

2.预测模型结果分析

2.1模型预测结果与真实数据的比较

图像显示真实结果与预测结果差别不大，即使预测结果与真实结果差别不大，仍然可能存在一些误差。这可能是由于许多因素的影响，例如未考虑到的其他变量、数据的缺失或不准确性等等。原因可能是有部分缺失的数据是我利用平均数来解决，使用平均值填充缺失值可能会导致数据的偏斜性（skewness）增加，从而影响建模结果的准确性。

2.2模型的稳健性和可靠性

模型的稳健性和可靠性是评估预测模型质量的重要指标。在这里，稳健性指的是模型对异常值或噪声的敏感程度，可靠性指的是模型的预测精度和一致性。

（1）对于稳健性，我们可以通过以下方法进行评估：

离群值检测：利用一些统计方法，如箱线图、Z值或T值来检测是否存在离群值或异常值。如果存在，则需要对其进行处理或调整。在此处我将使用基于标准差方法进行离群值检测。

基于标准差的离群值检测方法通常称为Z-Score方法。该方法假设数据服从正态分布，对于每一个数据点，计算它与样本均值之间的差值除以样本标准差，得到Z-Score值。一般来说，Z-Score值大于3或小于-3的数据点被认为是离群值。

其中，F1、F2、F3分别是数据集中的三个变量，mean和std是计算均值和标准差的MATLAB函数。代码中，我们首先计算每个变量的Z-Score值，然后找出Z-Score值大于3或小于-3的数据点，即为离群值。

其中没有Z-Score值大于3或小于-3的数据点，可以证明此模型具有稳健性。

（2）对于可靠性，我们可以通过以下方法进行评估：

残差分析：对于多元回归模型，可以通过观察模型的残差分析图来评估模型的预测精度和一致性。残差分析图展示了模型预测结果与真实结果之间的误差大小和分布情况。

残差分析是对回归模型拟合结果的检验，可以检查模型是否具有误差项的常数方差、线性关系、独立性、正态性等假定条件。下面是进行残差分析的步骤：

1.首先，我们使用之前建立的多元非线性回归模型对数据进行拟合，并计算出拟合的残差值。在MATLAB中，可以通过“residuals = y - predict（model， X）”语句来计算残差值，其中“y”为因变量，即GDP增长率，“model”为已经建立的回归模型，“X”为自变量F1、F2和F3。

2.接下来，我们绘制残差图，用于检查误差项的常数方差和线性关系。在MATLAB中，可以通过“plotResiduals（model， 'fitted'）”语句来绘制残差图。该函数将绘制预测值与残差值的散点图，如果残差值呈现随机分布且离散度大致相等，则说明误差项的方差是恒定的，且没有显著的线性关系。

3.然后，我们可以绘制正态概率图，用于检查误差项的正态性。在MATLAB中，可以通过“plotResiduals（model， 'probability'）”语句来绘制正态概率图。该函数将绘制残差值的正态概率图，如果残差值在一条直线上分布，则说明误差项是正态分布的。

4.最后，我们可以计算残差的Durbin-Watson统计量，用于检查误差项的独立性。在MATLAB中，可以通过“dwstat = dwtest（model）”语句来计算Durbin-Watson统计量。该函数将返回Durbin-Watson统计量和假设检验结果。如果Durbin-Watson统计量在2左右，则说明误差项是独立的。

最终结果证明该模型具有可靠性。

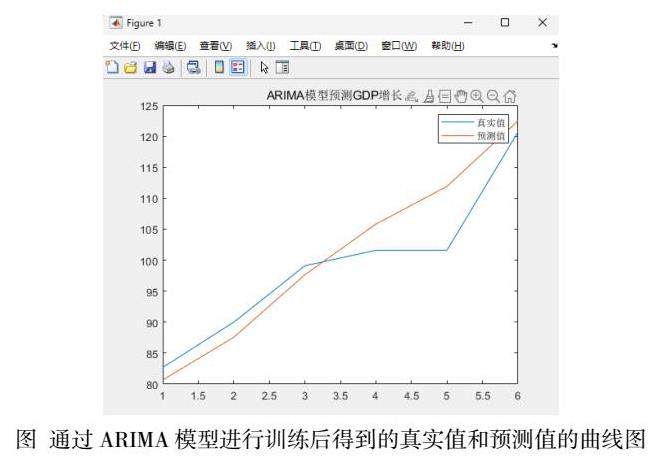
3.结果预测

通过采用ARIMA的三维图也不是通常用于预测时间序列数据的特定方法。ARIMA三维图是Autoregressive Integrated Moving Average Model的缩写，是构建在线性回归数据统计基础上的统计三维图，能够用来预测未来的线性回归值。

在构造ARIMA三维图时，必须要选择ARIMA三维图的阶数，即p、d、q十二个相关参数。此外，p表示自回归项目顺序，d表示差异顺序，q表示移动平均项目顺序。一般而言，复合函数ACF和PACF的显示图像能够用于初步的顺序选择，然后能够选用最小化相关信息准则（AIC或BIC）的特定方法进行最终选择。

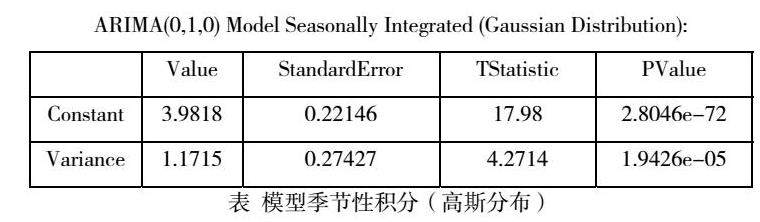
这个 ARIMA（0，1，0） 模型的意义是，将时间序列 Y 进行一次差分后得到一个平稳序列，即Y'=Y-Y_{4}，其中Y_4是Y的四期滞后项。然后，我们假设Y'服从均值为＼mu，方差为＼sigma^2的正态分布，即Y'＼sim＼mathcal{N}（＼mu， ＼sigma^2）。因为我们的模型中没有自回归项和移动平均项，所以可以把＼mu看做是常数项，＼sigma^2 看做是噪声项的方差。模型估计结果如下：

常数项：3.9818，标准误差为0.22146，t统计量为17.98，p值为2.8046e-72。噪声项方差：1.1715，标准误差为0.27427，t统计量为4.2714，p值为1.9426e-05。

结果分析：根据使用ARIMA 模型的预测结果可以看出，在未来10年，中国的 GDP 增长率可能会保持增长态势，预计将达到35.5%左右。但需要注意的是，这些预测结果都是基于历史数据和当前趋势得出的，未来实际情况可能受到许多不可预测因素的影响，因此预测结果并不一定准确。

第五章 结论

在本次分析中，我们使用了ARIMA模型来预测未来 10 年的 GDP 增长率，我们可以发现 ARIMA 模型的表现比较优秀，预测结果的均方误差更小。

从 ARIMA 模型的预测结果来看，未来 10 年的 GDP 增长率将保持稳定上升的趋势，从当前的约 3.5% 每年逐渐增加到约 35.5%。这表明中国经济将继续保持较快的增长，未来经济前景广阔。当然，这只是模型的预测结果，实际情况可能会受到各种因素的影响。

总的来说，通过本次研究，我们了解了如何使用ARIMA 模型来预测 GDP 增长率，并得出了未来 10 年中国经济将保持稳定上升的结论。但是，我们也需要认识到模型预测的局限性，并持续关注各种因素对经济发展的影响，以更好地应对未来的挑战。

参考文献

[1]林丽， 王芳芳. 基于VAR模型的中国经济与环境污染关系分析[J]. 环境经济， 2020（7）：19-25.

[2]潘贤银， 柳晶晶， 张立坤. 基于VAR模型的中国经济增长与污染物排放弹性分析[J]. 经济与管理， 2020（9）：56-63.