打开文本图片集

摘要：三轴转台在实际运行时，各个框架间会发生动力学耦合现象，并且受到的耦合力矩与各框架的转动惯量直接相关。本文针对三轴转台的框架惯量辨识，通过设计扩展卡尔曼滤波算法（EKF），得到了不同位姿下转台转轴的等效惯量，通过设计解算方法，辨识得到了各框架的惯量参数。

关键词：三轴转台；扩展卡尔曼滤波；惯量参数辨识

引言

三轴转台是模拟飞行器在空中姿态与运行轨迹的实验设备，可有效减少飞行器的实际飞行次数，在航空航天领域有着广泛应用。转台轴数越多，能够模拟的姿态和轨迹就越复杂。其中，三轴转台是一种典型的模拟飞行器的结构，通过三个轴的组合转动，可以模拟飞行器的偏航运动，俯仰运动和横滚运动。然而，三轴转台的控制精度会受到动力学耦合现象的限制，其耦合原因主要来源于惯量耦合和力矩耦合。其中，惯量耦合是由于转台在转动时，各框架在固定坐标系中欧拉角方位角变化导致的惯量向量的变化，进而使得框架转轴上的等效转动惯量发生变化，引起三个转轴上的惯量参数出现耦合现象。

针对转台参数辨识的相关算法有很多，如最小二乘法、梯度校正法、朗道离散递推辨识法以及卡尔曼滤波法等。其中，卡尔曼滤波算法能够在存在不确定性信息的运行环境下，估计出系统的实时状态，在控制、通信、图像等各个领域得到了广泛的应用。KF算法的缺陷是只能用于线性系统，为使其能够应用到更加常见的非线性系统，发展出了适用于非线性系统的扩展卡尔曼滤波（EKF）。本文采用EKF方法，针对三轴转台的框架惯量进行参数辨识，以有效改善转台的耦合现象，减小跟踪误差。

1、试验方法和试验方案

1.1 拓展卡尔曼滤波算法

1.2 框架惯量辨识

三轴转台的三个轴分别与各自的框架固连，设内框、中框、外框的惯量矩阵分别为。

由于三轴转台各个转轴上的等效惯量是由各框架的惯量分量所组合而成，所以我们先通过EKF对三轴转台各转轴的等效惯量进行参数辨识，然后再通过等效惯量和各框架的惯量分量的关系，反解求出各个框架的惯量。

2、试验方案

为了验证RBF神经网络自适应控制器的性能，本文使用MATLAB simscape搭建三轴转台动力学模型，三轴转台的结构如图1所示。

三轴转台的主轴1为外框旋转轴，绕着z轴旋转，主轴2为中框旋转轴，沿着y轴旋转，主轴3为内框旋转轴，沿着x轴旋转，其详细结构参数如表1所示：

本文定位精度要求为1角秒，对于EKF进行转台框架转动惯量参数辨识，制定了如下的仿真实验策略：

算法步骤：

信号发生器产生具有加速度信息的激励信号对系统进行激励。经过转台控制处理器后，激励信号转换为电机的控制电压，产生驱动力矩驱动转台转动。通过传感器测得的转轴实际转速和驱动力矩作为EKF算法的输入进行辨识，得到电机轴上的等效惯量。最后，通过多次测量不同位姿下的转轴等效惯量，再进行解算，即可得到进行耦合补偿所需要的7个框架转动惯量参数。

simulink仿真模型：

其中，模块一为速度激励信号发生器，由于需要加速度信息，使用正弦位置信号作为激励信号。模块二为转台控制器，模块三为电机仿真模型，模块四为联合仿真的三轴转台机械模型，模块五为外加的Stribeck摩擦模块，模块六为EKF参数辨识模块，模块七为惯量解算模块。

3、仿真结果与比较

3.1 EKF惯量辨识

本文需要辨识的各框实际转动惯量参数如表2所示：

通过EKF辨识法，对转台在不同位姿下进行惯量辨识，得到了如下的转轴等效惯量：

EKF对等效惯量的辨识结果如表3所示：

通过解算，得到各框架转动惯量参数的辨识结果，如表4所示：

由表4可知，EKF的辨识误差基本在1%以内，最大辨识误差为5.56%。整体辨识结果较高。

3.2 固定力矩法惯量辨识

为验证EKF辨识法的有效性，使用传统的固定力矩测量法进行对比实验。该方法的思路是：对框架给定固定的驱动力矩，测量其在单位时间后转台的角速度，通过以下公式得到等效惯量。

为保证对照实验的可靠性，对该方法测量得到的角速度，施加同样的测量噪声。

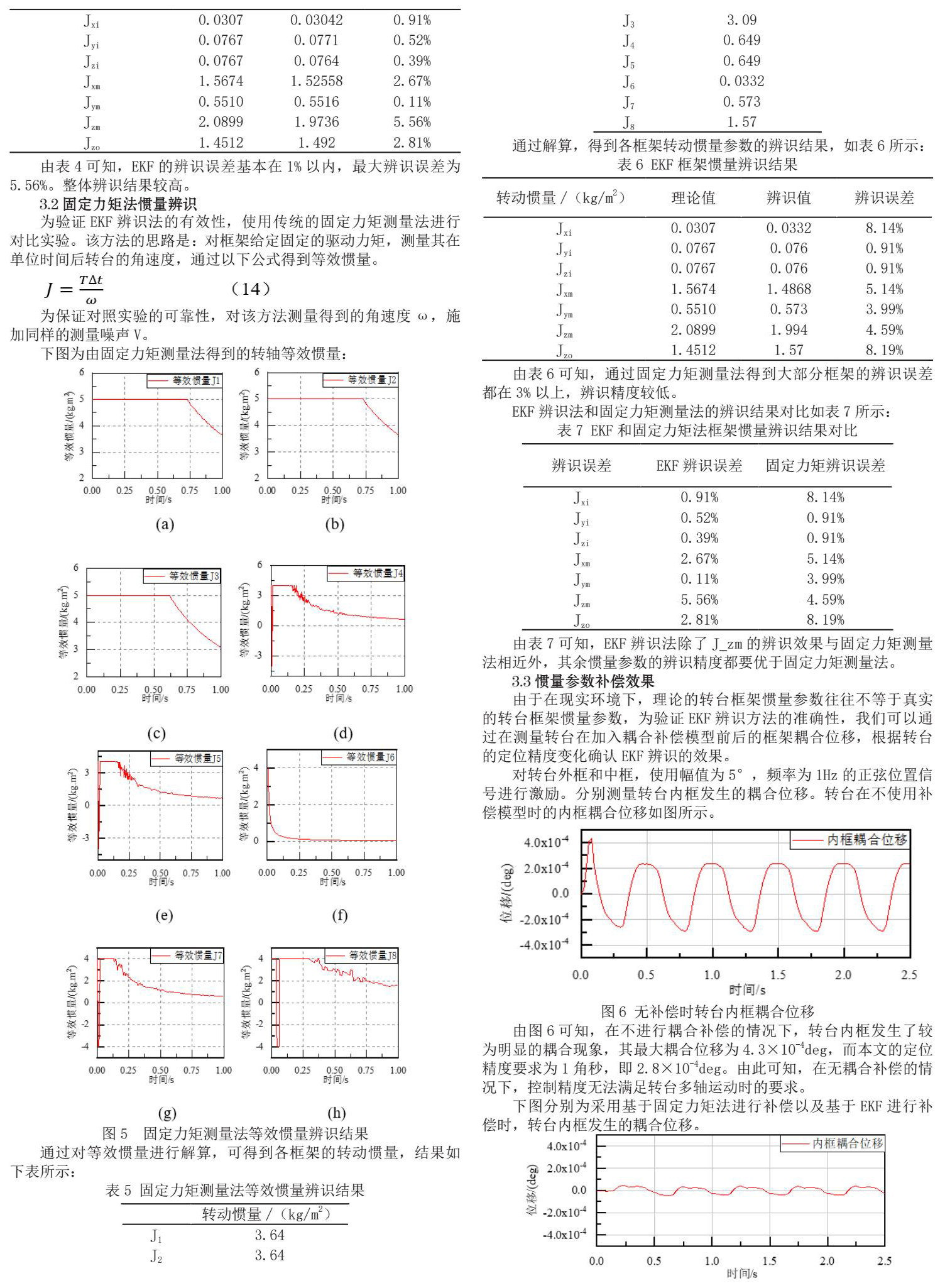
下图为由固定力矩测量法得到的转轴等效惯量：

通过对等效惯量进行解算，可得到各框架的转动惯量，结果如下表所示：

通过解算，得到各框架转动惯量参数的辨识结果，如表6所示：

由表6可知，通过固定力矩测量法得到大部分框架的辨识误差都在3%以上，辨识精度较低。

EKF辨识法和固定力矩测量法的辨识结果对比如表7所示：

由表7可知，EKF辨识法除了的辨识效果与固定力矩测量法相近外，其余惯量参数的辨识精度都要优于固定力矩测量法。

3.3 惯量参数补偿效果

由于在现实环境下，理论的转台框架惯量参数往往不等于真实的转台框架惯量参数，为验证EKF辨识方法的准确性，我们可以通过在测量转台在加入耦合补偿模型前后的框架耦合位移，根据转台的定位精度变化确认EKF辨识的效果。

对转台外框和中框，使用幅值为5°，频率为1Hz的正弦位置信号进行激励。分别测量转台内框发生的耦合位移。转台在不使用补偿模型时的内框耦合位移如图所示。

由图6可知，在不进行耦合补偿的情况下，转台内框发生了较为明显的耦合现象，其最大耦合位移为4.3×10-4deg，而本文的定位精度要求为1角秒，即2.8×10-4deg。由此可知，在无耦合补偿的情况下，控制精度无法满足转台多轴运动时的要求。

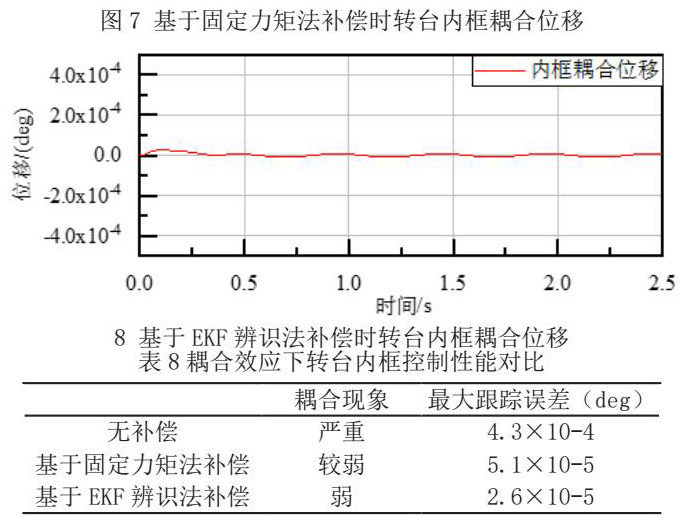
下图分别为采用基于固定力矩法进行补偿以及基于EKF进行补偿时，转台内框发生的耦合位移。

由图7和图8可知，在两种耦合模型的补偿下，转台的耦合位移均发生了下降，且基于EKF辨识法所得的耦合模型，相较于传统的力矩法，能够更好地降低转台发生的耦合位移，提高转台在多轴运动时的定位精度。在两种耦合模型的补偿下，内框的最大耦合位移分别为5.1×10-5deg以及2.6×10-5deg。下表为不同补偿方式下，转台的控制性能对比：

由表8可知，采用EKF辨识法所得的耦合模型能够有效改善转台的耦合现象，减小跟踪误差。相较于由固定力矩法所得的耦合模型，其补偿能力要更为优越。由此，完成了辨识算法有效性的验证。

4、结束语

针对三轴转台转轴上的惯量参数出现耦合现象导致影响控制精度的问题，提出了一种基于扩展卡尔曼滤波算法（EKF）的惯量参数辨识方法，得到了不同位姿下转台转轴的等效惯量。接着，通过设计解算方法，辨识得到了各框架的惯量参数。为验证该辨识方法的有效性，设计了基于固定力矩测量法的框架惯量辨识方法，用以进行对比实验。最后，仿真加入两种不同耦合补偿模型前后的框架耦合位移，以将理论分析和仿真实验结果分析结合研究了解决惯量参数耦合的问题，仿真实验结果表明，EKF具有更高的辨识精度。

参  考  文  献

[1] 雷雨龙， 付尧， 刘科， 等. 基于扩展卡尔曼滤波的车辆质量与道路坡度估计[J]. 农业机械学报， 2014， 45（11）： 9-13+8.

[2] 张云超， 刘昆. 三框架惯性稳定平台动力学分析[J]. 硅谷， 2011（20）： 145-147.

[3] 宋宏帅. 永磁同步电机转动惯量的辨识方法研究[D]. 齐鲁工业大学， 2019.

[4] 何晓会. 基于惯量辨识的永磁同步电机自抗扰控制策略研究[D]. 哈尔滨工业大学， 2020.

[5] Zhao Y， Qiu L， Zhang Y. Model-based friction compensation scheme for the linear inverted pendulum[C]. IEEE International Conference on Mechatronic Science， Electric Engineering and Computer （MEC）， Jilin， 2011： 554-558.

[6] Rigatos G G. Derivative-free Kalman Filtering for sensorless control of MIMO nonlinear dynamical systems[C]. IEEE International Conference on Mechatronics and Automation， Chengdu， 2012： 714-719.

[7]  Hu J， Xiong R . Contact Force Estimation for Robot Manipulator Using Semi-parametric Model and Disturbance Kalman Filter[J]. IEEE Transactions on Industrial Electronics， 2017， 65（4）： 3365-3375.