打开文本图片集

摘要：勾股定理是初中数学几何学习内容中的一个重要定理。本文基于对“勾股定理”探究课的设计，引导学生做真实性学习、做互助性学习、做文化性学习，于数学课堂中渗透数学核心素养，感受数学学习的魅力。

关键词：勾股定理；数学史；教学设计

数学是研究数量关系和空间形式的一门学科。勾股定理作为初中数学课程的重要内容之一，它兼具代数和几何的特征，在数与形之间架起了一座沟通的桥梁。中国最古老的数学著作《周髀算经》在数学上的主要成就是介绍并证明了勾股定理。因此，勾股定理的探索与验证向来是课堂教学的重点与难点。

一、教学内容分析

《勾股定理》是苏科版数学八年级上册第3章的起始课，它是在学生已经掌握了等腰三角形、直角三角形相关性质的基础上再学习的。勾股定理揭示的是直角三角形三边之间的数量关系，是解决直角三角形计算问题中的一条重要定理依据，在现实世界中具有广泛的应用。对后续学习实数，三角函数等也具有重要的思维铺垫作用。

当前教育正处于新课改的浪潮中，“核心素养”已取代“知识本位”，课堂是以学生为主体。八年级学生已具备一定的独立思考能力和探究能力。对于勾股定理的得出，需要学生在观察的基础上，大胆地猜想数学结论。过程中，学生小学虽已接触过割补法、面积法，但缺少与代数、推理的结合，如何由“数”到“形”，对于学生是难点。因此在本节课上注重引导学生自发完成对于定理的“观察—猜想—归纳—验证”过程，体会数形结合和由未知向已知转化的数学思想。让学生能结合问题情境，由特殊到一般，进而归纳总结出直角三角形三边之间的数量关系，体验数学家们发现勾股定理的过程，激发学习数学的兴趣，感受数学的魅力。

二、教学实践

（一）创设情境，问题引入

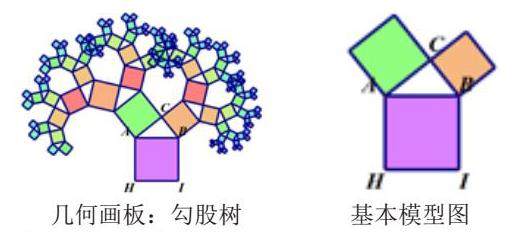
教师课前利用几何画板播放勾股树动画，上课之后静止动画。

问题1：你能从画面上感受到什么？

学生一致回答一棵树。

问题2：这棵“树”是由哪些数学的基本图形构成的？

学生一一回答，正方形和直角三角形。

问题3：你能否在这棵“勾股树”上找出一张基本模型图？

学生1上讲台在多媒体上勾出模型。

教师：这位同学找的特别棒！今天我们就来研究这张基本图形上的面积问题。

教师将勾股树参数设为1，出现基本模型图。

【设计意图】

利用几何画板制作精美的“勾股树”动画在课前播放，让学生感受勾股定理蕴藏的数学之美，激发学生对本节课内容探讨的积极性。通过静止画面，学生进一步观察发现组成勾股树的基本模型图，引出本节课讨论内容。发现过程遵循了学生的客观认知过程，由学生自主完成的。

（二）利用网格，猜想定理

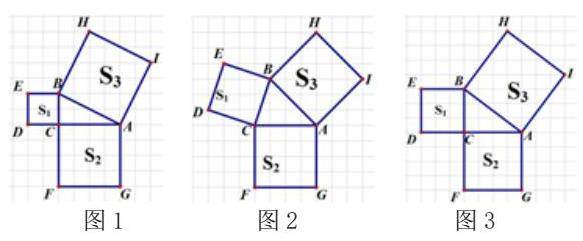
活动1  将基本模型图经过一定旋转，放进每个小方格都是边长为1的正方形的网格纸中，两条直角边正好在网格线上，借助网格的特征，观察下列3张图，你能有哪些发现？

1.你能求出这三张图中三个正方形的面积吗？

2.这几张图中三块正方形的面积之间有怎样的数量关系？

3.它们与直角△ABC的三条边又有何关系？

教师先让学生独立思考，在活动单上探究完成（5分钟），再小组讨论（2分钟），最后请学生小组代表上台展示汇报。

（1）计算探究

问题1：你能求出这三张图中三个正方形的面积吗？

学生2：第（1）小问，在图1中，S1=4，S2=16，S3=20；图2中，S1=10，S2=16，S3=18；图3中，S1=9，S2=16，S3=25。（学生在回答“不友好”的正方形面积结果时有点不确定。）

教师及时予以结果的肯定，同时抛出质疑，对于边长不在网格线上的“不友好”的正方形面积的求解方法。

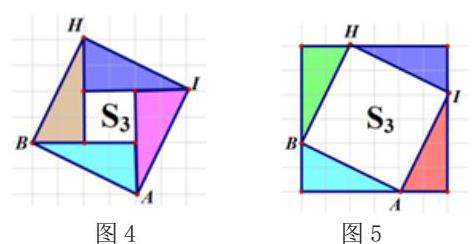
学生3：（上台用实物投影展示）以图1中的S3为例，将“不友好”的正方形分割成4个全等的直角边长在网格线上的直角三角形和一个边长在网格纸上的小正方形（图4）。4个直角三角形的面积利用网格计算就是16，小正方形的面积是4，所以S3=20。其他几个“不友好”正方形的面积也是像这样利用网格线分割之后计算得到的。

教师：这组同学是用到了“割”的方法，将“不友好”正方形的面积转化成了4个友好的直角三角形和一个正方形求解的。还有其他计算的方法吗？

学生4：（其他小组代表上实物投影展示）可以用“补”的方法。还是以图1中的S3为例，在这个“不友好”的正方形外面利用网格线补出一个新的大正方形（如图5）。此时S3等于新的大正方程面积减去周围四只全等的直角三角形面积，也可以得到S3=20。

教师总结归纳利用“割补法”求“不友好”图形的面积，由未知转化为已知。

（2）归纳发现

问题2：这几张图中三块正方形的面积之间有怎样的数量关系？

学生5：我们发现在图1和图3中的三角形都是直角三角形的情况下，有S1+S2=S3。

教师：能否用文字语言叙述？

学生5：以直角三角形两条直角边长作的正方形的面积和，等于以这个直角三角形斜边长作的正方形的面积。

（3）提出猜想

问题3：这个发现与直角△ABC的三条边又有何关系？

学生6：正方形的面积是通过边长的平方得到的，这三个正方形面积之间的等量关系可以转换成这个直角三角形三条边长间的数量关系。

教师与学生共同归纳得到关于直角三角形三边关系的一个猜想：直角三角形两条直角边的平方和等于斜边的平方。

教师板书结论。

【设计意图】

把“勾股树”中的基本模型图搬到网格中方便学生探讨。其中有正方形面积是可以利用网格线直接求解的，也有“不友好”的正方形。把不能利用网格计算面积的“不友好”图形，利用“割补法”转化成可以利用网格线直接计算面积的图形，在学生心中种下转化的数学思想，教会学生如何用数学思维思考。整个过程，学生经历从特殊到一般，从猜想到验证的活动过程，提升了数学学习能力。在第（1）题的计算基础上，自然能得出三个正方形面积的关系，从而得到直角三角形中的三边关系。图2设计了一只锐角三角形，既是为了帮助学生强调勾股定理研究的是直角三角形的三边关系，也是埋了一个“彩蛋”，锐角三角形、钝角三角形的两边的平方和和第三边的平方和之间的数量关系是怎么样的？

（三）感受历史，体会定理

从活动1的探究中，我们发现了数的平方可以在正方形的面积中体现，将数与形结合了起来。这个重大的发现其实在我国公元前1世纪就有人发现了，并给它取名“勾股定理”。（板书课题）

教师出示2则微视频，介绍关于中西方关于勾股定理的趣味故事。

【设计意图】

勾股定理是几何学上的重要定理，凝聚着中西方优秀的数学历史文化。在课堂中穿插数学史，可以让学生感受到勾股定理丰富的理论内涵，体会到中国古人的创新精神，激发起学生民族自豪感和中华文化的认同感；也可以帮助学生加深对数学知识、数学思想的理解，从而更好地促进学生的核心素养的生成。

（四）动手实践，验证定理

活动2：若是将网格纸去掉，变成一个一般的直角三角形，你能借用今天研究的正方形的面积法验证上面的公式吗？

教师让学生以小组为单位，通过拼接4个全等的直角三角形，设计出一种方案来验证猜想。完成之后以小组为单位上讲台展示。

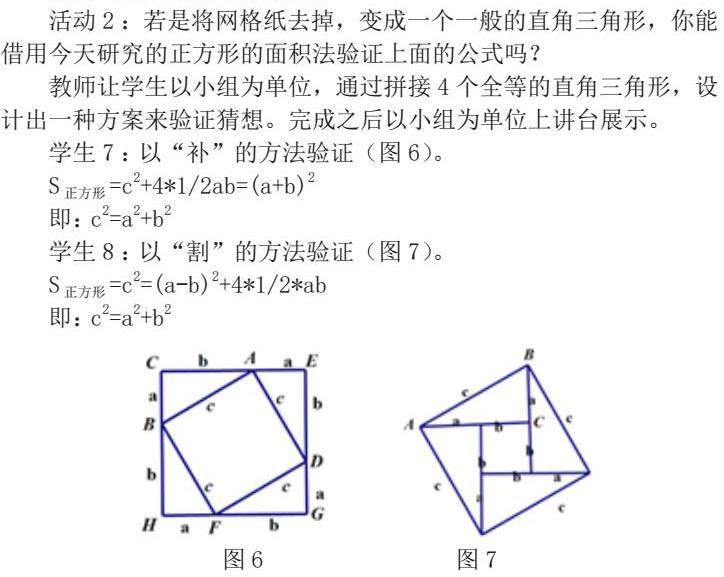
学生7：以“补”的方法验证（图6）。

S正方形=c2+4*1/2ab=（a+b）2

即：c2=a2+b2

学生8：以“割”的方法验证（图7）。

S正方形=c2=（a-b）2+4*1/2*ab

即：c2=a2+b2

【设计意图】

有了问题1的思维铺垫，学生在这个环节能很顺滑地拼出图形，并利用面积恒等与数形结合的方法，验证直角三角形三边的数量关系，从而论证勾股定理。在这个过程中，教师充分将主动权归还给学生，满足学生探究的欲望，帮助他们真正掌握数学知识背后的本质。让学生汇报展示，鼓励学生学会用数学的语言表达他们的发现，更好地在课堂落实数学核心素养的培养。

（五）总结

1.利用网格图了解了千古第一定理——勾股定理。

2.通过实践拼图证明了直角三角形具有两直角边的平方的和等于斜边的平方。

3.勾股定理的证明方法千千万万，同学们可以趁着课余时间去了解。

【设计意图】

在回顾整合中，萃取精华，帮助学生做好定理学习的活动经验积累。同时做好课后学习的引导，培养学生课堂外学习的能力。

三、教学回望

（一）独立探究，做真实性学习

“授人以鱼不如授人以渔。”勾股定理的背后蕴含着中西方数学家们的数学思想，想要习得数学家们的结论，就要能像数学家们一样思考，会用数学的眼光思考世界。在课堂上，学生需要在教师问题的导引下抽丝剥茧，由简入繁，由易到难，由表层到深入，于无形之中学会思考，好像是在走一个螺旋式上升的楼梯，看似还在原地打转儿，实则已经离开了那一个平面，达到了真实性学习。

本节课主要是勾股定理的一个探究性学习，教师从“勾股树”模型出发，提出问题，引发学生对勾股定理的基本模型图的思考。从网格图形中探求面积关系，从面积关系中构建直角三角形的三边关系，从猜想定理到证明定理，一个个问题接连抛出，引发学生思考问题，探究问题背后的数学思想。这样的探究性学习，既能调到学生的思维，又能渗透数学核心素养，达到真实性学习的目的。

（二）小组合作，做互助性学习

在数学课堂教学中，为落实学生数学核心素养的培养，除了帮助学生做好独立的真实性学习，还需培养学生的合作交流能力，会用数学的语言表达。奥斯特洛夫斯基说，不管一个人多么有才能，但是集体常常比他更聪明和更有力。小组合作就是将学生的智慧集中起来，小组成员带着自己独立思考之后的结果，提出自己的困惑，进行思维碰撞，进而能从不同角度来思考和解决问题，使解决问题的方案越来越合理化。

在本堂探究课中设计了两处小组合作，分别在定理的猜想和验证环节。定理的猜想是通过分别计算3张放置在网格图中的模型图中，不同的正方形面积得到的。由于学生学习能力的差异，并不是班级所有学生都能得到正确结论。通过小组合作，学生能在组内交流中互相学习，发现最优解法，也能及时发现计算失误，避免由计算失误而影响到对定理的猜想。在验证环节，每个人手中只有一张直角三角形卡片，小组合作拼接的目的一是节省时间，二也是为了渗透合作意识。

（三）体验历史，做文化性学习

马赫曾说过，没有任何科学教育可以不重视科学的历史与哲学。数学史刻画了数学家们从发现问题到解决问题一步步的探索琢磨过程，以及在漫长研究过程中对已获取知识到未知领域的跨越。数学史融入课堂教育不仅能吸引学生注意力，调动学生学习的兴趣与激情，消除学生对数学的畏惧感与枯燥乏味的无趣性，拉近学生与数学的距离，更可以在教师的指导下重新经历数学家们的创造过程，保证思维的连续性，补全数学思想方法的空白。

勾股定理从古至今一直在散发它的魅力，任何一本几何教科书上都有它的身影，其中蕴含的育人价值是不可言喻的。漫漫历史长河中，我国早在公元前1100年的《周髀算经》中就有“勾广三，股修四，经隅五”的叙述，而公元前六世纪古希腊数学家毕达哥拉斯才从地板图案中发现了这一定理。公元前三世纪欧几里得的《几何原本》中出现几何演绎的证明方法，公元三世纪中国的赵爽弦图、公元250年刘徽的青朱入出图紧跟其后，目前对于勾股定理的证明方法已达到500多种。数学的博大精深都是由无数先辈的智慧堆积而成的，勾股定理数学史的介绍可以帮助培养学生的民族自豪感和赤诚之心，以先辈们严谨的科学态度和锲而不舍的创新精神为养料，培育出不断追求自身进步、不断超越自我的新一代青少年。

参考文献

[1]刘颖超。吴立宝。指向核心素养的勾股定理教学设计[J]。中学数学教学，2022，（03）：31-35。

[2]余旭红。“德育”融入数学课堂的实践与思考——以“探索勾股定理”教学为例 [J]。初中数学教与学。2022，（09）：20-22。

[3]中华人民共和国教育部。义务教育数学课程标准（2022年版）[M]。 北京：北京师范大学出版社，2022。