打开文本图片集

摘要：本文通过建立二阶线性非齐次微分方程模型求解波浪能装置最大输出功率，根据牛顿第二定律，以及相关的能量转化知识、物体间的耦合作用知识建立数学相关模型，通过4，5阶龙格-库塔法，进行结果求解得出结果，通过灵敏性分析等验证方法对实验结果进行验证。

关键词：垂荡-纵摇耦合运动；4，5阶龙格-库塔法；转动定律；二阶非线性非齐次微分方程

引言：

波浪蕴涵能量巨大，能量密度高，波浪能装置由浮子、中轴、中轴底座、振子、隔层及能量输出系统PTO（由弹簧、直线阻尼器构成）组成。在波浪作用下，浮子会带动振子运动，通过两者的相对运动使直线阻尼器做功，并将所做功以能量形式输出。

1模型的建立与求解

1.1问题一模型的建立与求解

1.1.1浮子和振子运动模型的建立：

对浮子进行受力分析，浮子受静水恢复力，波荡激励力和附加惯性力，由于重力比流体冲击力小很多，以此忽略重力。根据牛顿第二定律，得出浮子的运动模型-二阶线性非齐次微分方程模型：

式（1）中：m1为浮子质量，M为附加质量，s0横截面水线截面积，z1为浮子相对位移，f为波浪激励力振幅，w为波浪频率，c为兴波阻尼系数。

2振子运动模型的建立

对振子进行受力分析：弹簧阻力、直线阻尼器阻尼力、重力。

根据牛顿第二定律，得出振子运动模型-二阶线性非齐次微分方程模型：

两种情况下浮子和振子垂荡位移和速度的求解

1．情况一，当直线阻尼器的阻尼系数为10000N·s/m时，将阻尼系数带入振子公式（2）得：

2．情况二，因阻尼器的阻尼系数与浮子和振子的相对速度的绝对值的幂成正比，幂取0.5，比例系数为10000，得情况二中振子运动模型公式：

1.1.3模型的计算结果：

（1）针对情况一：

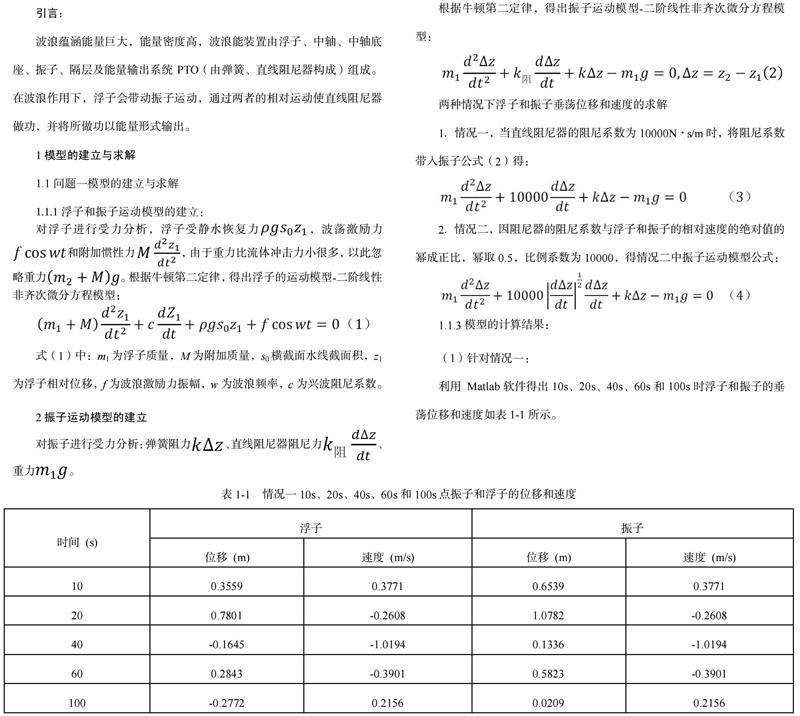
利用 Matlab软件得出10s、20s、40s、60s和100s时浮子和振子的垂荡位移和速度如表1-1所示。

可以分析出，5.2s后振子和浮子以0.2980m的距离且速度相同保持相同的运动状态。

（2）针对情况二：

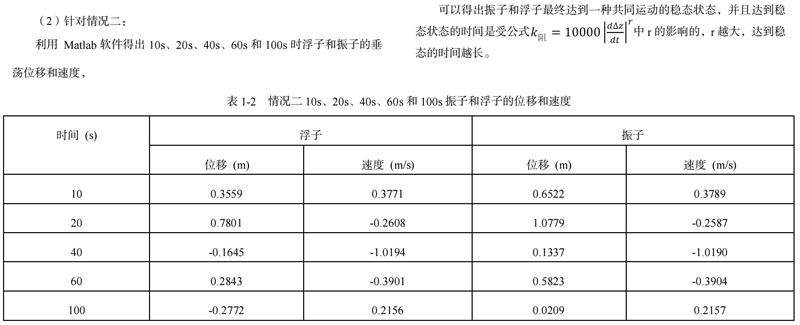
利用 Matlab软件得出10s、20s、40s、60s和100s时浮子和振子的垂荡位移和速度，

可以得出振子和浮子最终达到一种共同运动的稳态状态，并且达到稳态状态的时间是受公式中r的影响的，r越大，达到稳态的时间越长。

1.2问题二模型的建立与求解

1.2.1模型的建立：

（1）情况一：阻尼系数为常量，阻尼系数取值范围为[0，100000]。

在波浪中浮子仍只做垂荡运动，直线阻尼器的阻尼力与浮子和振子的相对速度成正比，比例系数仍为直线阻尼器的阻尼系数，所以得到P关于v的方程：

为振子相对于浮子的位移。

（2）情况二：阻尼系数与浮子和振子的相对速度的绝对值的幂成正比，比例系数取值范围为[0，100000]。得到情况二积分模型：

模型的求解：

情况一的求解：

第一步：使用for循环给阻尼系数分步长进行赋值，并且步长为500。

第二步：在给赋值的每一步中进行时间的步长赋值，这里采用的范围为[0～40T]，步长为0.1s。

第三步：求解每一步中的微分方程，得出振子和浮子的相对速度，即为一阶导数。

代入公式（9）中计算k值对应的p值。

第四步：把第三步中的结果代入公式（13）中计算40个周期内的平均功率。

第五步：根据前四步，可以得到的数据组。

第六步：根据第五步得到的数据组，进行函数图像的描述。

第七步：结果分析：根据图像可知，最大功率为123.0270w时，对应的最优阻尼系数为37688.4422N·s/m。

情况二的求解：

第一步：建立双层循环中的外循环第二步：建立双层循环中的内循环

第三步：对幂指数r和比例系数k两个参数进行参数循环。

第四步：用4，5阶龙格-库塔算法解出相对速度。

第五步：把第四步得到的相对速度带入公式（9）中求解功率p。

第六步：得到对应的平均功率。

第七步：重复前六步得到，幂指数r和比例系数k与平均功率的对应数据组。

第八步：得出函数图像

第十步：结果分析：根据图像可知在平均最大功率为123.0263w时，对应的最优阻尼系数为37373.7374N·s/m。

参考文献

[1]何孔德，谢旭光，方子帆，杨蔚华.水下系泊监测平台垂荡纵摇耦合运动特性分析[J].科技通报，2017，33（01）：123-128.DOI：10.13774/j.cnki.kjtb.2017.01.027

[2]高琅，朱良生，王磊，周斌珍.垂荡式波浪能装置与风机平台集成系统水动力性能研究[J].广东造船，2022，41（03）：17-21.

[3]黄伟.直驱式波浪发电系统的功率捕获控制技术研究[D].华南理工大学，2021.

论文来源：2022年“高教社杯”全国大学生数学建模竞赛。