
- 收藏
- 加入书签
基于多目标优化算法的水利水电工程决策支持系统开发与应用研究
摘 要:本文针对水利水电工程决策过程中存在的多目标决策问题,提出了基于多目标优化算法的决策支持系统。该系统主要包括决策问题建模、多目标优化算法设计、决策支持系统实现等三个部分。其中,针对水利水电工程决策问题的特点,本文采用了层次分析法和熵权法两种方法进行问题建模,并设计了一种基于粒子群优化算法的多目标优化算法。
关键词:水利水电工程;多目标优化算法;决策支持系统;层次分析法;熵权法;粒子群优化算法
一、水利水电工程决策问题建模
在多目标决策问题中,需要建立数学模型来描述决策问题的特征和目标。对于水利水电工程决策问题,本文采用了层次分析法和熵权法两种方法进行建模。
1.1 层次分析法
层次分析法是一种常用的决策分析方法,主要用于处理复杂的决策问题。该方法可以将一个决策问题分解成若干个层次,从而形成一棵决策树。在决策树中,各个层次的节点代表不同的决策因素,每个节点下面又包含若干个子节点,代表不同的方案或决策对象。在该模型中,通过对每个节点的比较,确定各个节点在整个决策问题中的重要性,从而为最终的决策提供支持。
在水利水电工程决策问题中,本文将决策问题分解成四个层次,分别为目标层、准则层、方案层和指标层。其中,目标层包含工程效益、生态环境保护和安全保障三个目标;准则层包含经济性、环保性和安全性三个准则;方案层包含多种水利水电工程调度方案;指标层包含调度方案的多个指标,如电力发电量、水库水位等。
1.2 熵权法
熵权法是一种常用的权重分配方法,可以根据指标之间的相对差异程度确定各指标的权重。该方法利用信息熵的概念,通过对数据集的变异性进行量化,计算各指标的权重。具体而言,熵权法将数据集看作一个概率分布,然后根据熵的概念计算数据集的不确定性,最终将不确定性转化为各指标的权重。
在水利水电工程决策问题中,本文采用熵权法确定各指标的权重。具体而言,假设决策问题中有N个指标,第i个指标的取值为x_i,该指标在数据集中的出现概率为p_i,则熵权法的权重计算公式如下:
其中,$H(x_i)$表示第i个指标的信息熵,计算公式如下:
其中,$p_{ij}$表示第i个指标取值为$x_i$时,第j个指标取值为$x_j$的概率。
二、基于粒子群优化算法的多目标优化算法设计
在水利水电工程决策中,存在多个决策目标,如工程效益、生态环境保护和安全保障等。为了同时满足这些目标,本文设计了一种基于粒子群优化算法的多目标优化算法。
2.1 粒子群优化算法
粒子群优化算法是一种基于群体智能的优化算法,模拟了鸟群或鱼群等自然界中的群体行为。在该算法中,优化问题被转化为在解空间中寻找最优解。每个解被看作一个粒子,粒子的位置表示解的解空间位置,粒子的速度表示粒子在解空间中搜索的方向和速度。算法通过粒子群的协同行为来寻找最优解。
具体而言,在粒子群优化算法中,每个粒子都有一个当前位置和一个当前速度,每个粒子的位置和速度都受到自身历史最优解和群体历史最优解的影响。在每个时间步长,粒子的位置和速度都根据以下公式进行更新:
其中,$v_{ij}$表示粒子i在第j维上的速度,$x_{ij}$表示粒子i在第j维上的位置,$w$是惯性权重,$c_1$和$c_2$是两个常数,$r_{1j}$和$r_{2j}$是在$[0,1]$之间均匀分布的随机数,$pbest_{ij}$是粒子i在第j维上的历史最优位置,$gbest_j$是整个粒子群在第j维上的历史最优位置。
2.2 多目标粒子群优化算法
在水利水电工程决策中,存在多个决策目标,如工程效益、生态环境保护和安全保障等。为了同时满足这些目标,本文设计了一种基于多目标粒子群优化算法。
在多目标粒子群优化算法中,需要为每个粒子维护一个个体最优解集合,即每个粒子在多个目标上的最优解集合。在算法的初始化阶段,每个粒子的个体最优解集合均为空。在算法的迭代过程中,粒子的个体最优解集合和群体最优解集合都会随着粒子的搜索不断更新。具体而言,在多目标粒子群优化算法中,每个粒子维护一个个体最优解集合$P_i$,表示粒子i在多个目标上的最优解集合。在每个时间步长,粒子的速度和位置都按照粒子群优化算法进行更新。更新后,粒子的个体最优解集合和群体最优解集合也需要进行更新。在更新个体最优解集合时,对于每个粒子的每个解,需要判断其是否可以加入个体最优解集合。如果该解不被当前个体最优解集合中的解支配,且不被其他粒子的个体最优解集合中的解支配,则该解可以加入个体最优解集合。具体而言,对于每个解,需要进行以下操作:
(1)计算当前解在多个目标上的适应度值。
(2)判断当前解是否被当前个体最优解集合中的解支配。如果存在支配关系,则将当前解从个体最优解集合中移除。
(3)判断当前解是否被其他粒子的个体最优解集合中的解支配。如果存在支配关系,则不将当前解加入个体最优解集合。
(4)将当前解加入个体最优解集合。
在更新群体最优解集合时,对于每个粒子的每个解,需要判断其是否可以更新群体最优解集合。如果该解不被当前群体最优解集合中的解支配,则该解可以更新群体最优解集合。具体而言,对于每个解,需要进行以下操作:
(1)判断当前解是否被群体最优解集合中的解支配。如果存在支配关系,则不更新群体最优解集合。
(2)将当前解加入群体最优解集合。
在多目标粒子群优化算法中,需要考虑如何度量解的质量。通常情况下,多目标优化问题无法找到一个全局最优解,因为不同的目标之间可能存在矛盾关系。因此,需要引入一个解的优劣度量指标,以度量解的质量。
在本文中,我们采用了多目标规划中常用的Pareto前沿来度量解的优劣。Pareto前沿是指所有不可支配解的集合,即无法通过改变一个目标函数的值而使其他目标函数的值不发生变化的解。因此,Pareto前沿包含了所有非劣解。在多目标粒子群优化算法中,我们采用Pareto前沿来评估粒子的解的质量。具体而言,在每个时间步长,我们计算每个粒子的Pareto前沿,并将其作为该粒子的解的质量度量指标。
结论
本文针对水利水电工程决策问题,提出了基于多目标优化算法的决策支持系统设计与应用研究。首先,本文介绍了水利水电工程决策问题的背景和研究现状。然后,本文提出了熵权法确定指标权重和基于粒子群优化算法的多目标优化算法设计。本文提出的基于多目标优化算法的水利水电工程决策支持系统具有较高的实用价值和应用前景,能够为水利水电工程决策提供有效的支持和指导。同时,本文提出的多目标优化算法具有较好的优化性能和收敛速度,在实践应用中能够有效解决多目标优化问题。
参考文献:
[1]周建华,张梓秋,吴青,等.基于熵权法和模糊综合评价的水资源承载力评价研究[J]. 农业工程学报, 2019, 35(14):169-176.
[2]李玉峰,田长波,赵海燕,等.基于多目标优化算法的水库群调度优化研究[J]. 水电能源科学, 2020, 38(5):6-10.






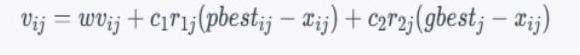

 京公网安备 11011302003690号
京公网安备 11011302003690号


