打开文本图片集

一、学生起点分析

八年级学生已经具备一定的观察、归纳、探索和推理的能力．在小学，他们已学习了一些几何图形面积的计算方法（包括割补法），但运用面积法和割补思想解决问题的意识和能力还远远不够．部分学生听说过“勾三股四弦五”，但并没有真正认识什么是“勾股定理”．此外，学生普遍学习积极性较高，探究意识较强，课堂活动参与较主动，但合作交流能力和探究能力有待加强．

二、教学任务分析

本节课是义务教育课程标准实验教科书北师大版八年级（上）第一章《勾股定理》第一节第1课时. 勾股定理揭示了直角三角形三边之间的一种美妙关系，将形与数密切联系起来，在数学的发展和现实世界中有着广泛的作用．本节是直角三角形相关知识的延续，同时也是学生认识无理数的基础，充分体现了数学知识承前启后的紧密相关性、连续性．此外，历史上勾股定理的发现反映了人类杰出的智慧，其中蕴涵着丰富的科学与人文价值。

三、教学目标：

1．经历用数格子的办法探索勾股定理的过程，进一步发展学生的合情推理意识，主动探究的习惯，进一步体会数学与现实生活的紧密联系．

2．探索并理解直角三角形的三边之间的数量关系，进一步发展学生的说理和简单推理的意识及能力．

核心素养：培养独立思考的习惯和能力；培养学生合作交流探究能力及语言表达能力；培养学生大胆尝试勇于挑战的能力。

四、重点、难点

重点：勾股定理的由来并能用它解决一些简单问题．

难点：勾股定理的探索．

五、教学过程

第一环节、创设情境，导入新课

出示投影1美丽的勾股树中蕴含着数学知识，开门见山，直接引出课题．这就是我们这一节要探究的问题：勾股定理．

第二环节、合作交流，探究新知

1．做一做：

四人一小组，拿出准备好的纸，画出一些直角三角形，分别测量它们的三条边，合作、交流看看三边长的平方之间有什么样的关系？与同伴交流．

2．探究与发现：

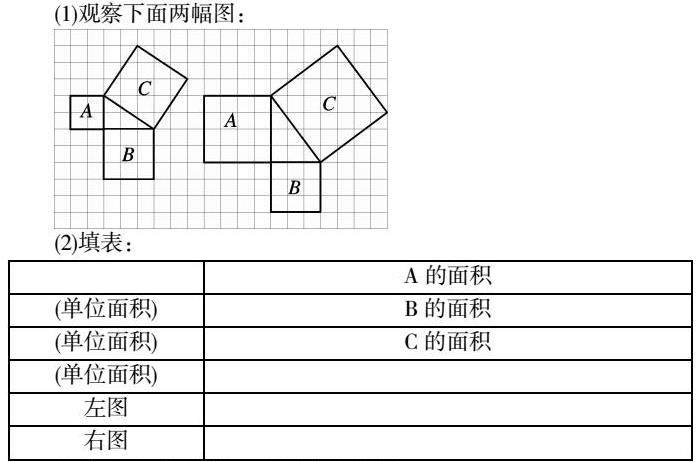
（1）观察下面两幅图：

（2）填表：

（3）分析填表的数据，你发现了什么？

学生通过分析数据，归纳出：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积．

3．议一议：

（1）你能用直角三角形的边长a，b，c来表示上图中正方形的面积吗？

（2）你能发现直角三角形三边长度之间存在什么关系吗？

在同学的交流基础上，教师板书：

直角三角形两直角边的平方和等于斜边的平方．这就是著名的“勾股定理”．

也就是说：如果直角三角形的两直角边为a，b，斜边为c，那么a2＋b2＝c2.

我国古代称直角三角形的较短的直角边为勾，较长的为股，斜边为弦，这就是勾股定理的由来．

第三环节、例题学习

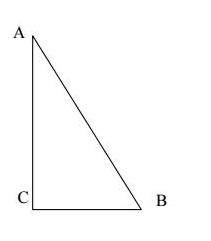
例： 如果直角三角形两直角边长分别为BC=5厘米 ， AC=12厘米，求斜边AB的长度.

（教师板演解题过程）

通过引例的探究，让学生知道勾股定理的内容，同时也让学生明白如何利用勾股定理来解题，尤其是解题过程如何书写

第四环节、运用新知，深化理解

（一） 基础训练：

1．求下列图形中未知正方形的面积或未知边的长度（口答）：

2． 一高为2.5米的木梯，架在高为2.4米的墙上（如图），这时梯脚与墙的距离是多少？

（二）能力提升：

已知∠ ACB=90°，CD⊥AB AC=3，BC=4. 求CD的长

第五环节、解决问题：

小明妈妈买了一部29 in（74 cm）的电视机，小明量了电视机的屏幕后，发现屏幕只有58 cm长和46 cm宽，他觉得一定是售货员搞错了．你同意他的想法吗？你能解释这是为什么吗？

六、交流小结，梳理知识与收获

让学生通过本节课的学习，自己归纳本节课的知识要点，学会了什么？还有哪些交流与困惑？

七、布置作业：

分层布置：必做题与选做题