打开文本图片集

摘  要：TRIZ理论是源于技术领域的“发明问题的解决理论”，其创新价值已被世界500强企业广泛认可。将技术领域中的TRIZ理论应用到管理领域中，尤其是应用到学校的教育教学管理领域中，是TRIZ理论新兴的研究方向，虽然目前研究文献数量偏少，但几乎覆盖了90%的TRIZ理论的知识点。论述了在中国知网中TRIZ理论的调研统计结果。近三年的相关文献显示，TRIZ理论的融合场景或切入点可以分为四类：单门课程教学、创新创业教育、学科专业建设、教育教学管理。提出了“五级制学习复杂度模型”并给出了算例。为便于日后解决学校教育教学管理问题，文中提出融合树模型。研究表明：TRIZ理论的基本思想和方法也可以应用到学校的教育教学管理领域，是推动学校高质量发展的重要手段。

关键词：教育管理;教学管理;TRIZ理论;学习复杂度模型;融合树模型

中图分类号：G642.0     文献标志码：A

TRIZ理论是苏联发明家根里奇·阿奇舒勒（G.S.Altshuller）在1946年创立的发明问题解决理论，是一种可创新性解决技术问题的重要工具方法，以其普遍性、可操作性和实用性，被高校广泛的引入教学培养体系。[1]麻省理工学院的一项实验数据表明，学习TRIZ理论的学生比没有学习该理论的学生创新能力提高了近一倍。[2]TRIZ理论源于技术领域，虽然技术领域与高校教育教学管理领域具有一定的差异性，但近三年的研究成果表明：TRIZ理论的基本思想和方法也可以应用到学校的教育教学管理领域，是推动学校高质量发展的重要手段。

一 基于中国知网的文献调研

2022年8月3日在中国知网（www.cnki.net）中的检索条件及其结果如下：

检索条件：“主题=TRIZ”AND“时间范围=2000.01.1～2022.07.31”。

检索结果：共有7990篇文献，其中学术期刊5867篇、学位论文1203篇、会议论文438篇、报纸79篇。主要涉及的主题有：TRIZ理论（1076篇）、创新设计（601篇）、TRIZ（404篇）、创新方法（338篇）。主要涉及的学科有：工业通用技术及设备（1021篇）、企业经济（1017篇）、机械工业（730篇）、计算机软件及计算机应用（649篇）、高等教育（567篇）。年发文量400篇（含）以上的年度有：2011（527篇）、2012（487篇）、2013（547篇）、2014（554篇）、2015（714篇）、2016（646篇）、2017（619篇）、2018（560篇）、2019（567篇）、2020（569篇）、2021（478篇）。发文量累计100篇（含）以上的文献来源有：《科技创新与品牌》（181篇），《河北工业大学》（154篇），《Procedia Engineering》（151篇），《包装工程》（144篇），《黑河学院学报》（112篇），《机械设计》（100篇）。国内发文量前五名的作者是：檀润华（102篇）、赵新军（41篇）、任工昌（39篇）、成思源（35篇）、邓援超（30篇）。国外发文量前五名的作者是：Denis Cavallucci（33篇）、Gaetano Cascini（26篇）、Davide Russo（19篇）、Francois Rousselot（17篇）、Federico Rotini（14篇）。发文量前六名的机构有：河北工业大学（378篇）、东北林业大学（110篇）、广东工业大学（107篇）、东北大学（91篇）、华南理工大学（90篇）、黑河学院（89篇）。发文量前六名的基金有：国家自然科学基金（624篇）、中央级科研院所科技基础性工作专项资金项目（67篇）、国家科技支撑计划（61篇）、河北省自然科学基金（51篇）、国家高技术研究发展计划（863计划篇）（50篇）、国家社会科学基金（40篇）。

如果进一步限定主题为“教学管理”或“教育教学”，则检索结果仅为：36条，不足总数的5‰，且大都集中在近三年里，这说明：基于TRIZ理论的高校教育教学管理方面的研究成果偏少，处于萌芽研究阶段，是TRIZ理论中新兴的研究热点。

二 文献调研分析

经研究分析，近三年的相关文献的融合场景或切入点可以分为四类。

第1类：将TRIZ理论融入单门课程教学中

孙晓[1]等人（2019）在《电力系统自动化》课程中应用TRIZ理论中的因果链分析工具找出了解决静电危害的可能途径、用剪裁原理设计出用发动机加热的汽车暖风系统、用物-场模型分析了电力系统的四种调压方法。

朱妍雯[3]等人（2019）在《电工学》课程中引入TRIZ理论：认为电子器件、电子线路的发展遵循着技术系统的S进化曲线法则;用技术系统中提高理想度的法则分析了从真空管电子电路到超大规模集成电路的进化过程。

郁佳佳[4]等人（2019）基于TRIZ创新理念，从更新课堂教学模式（动态化原理）、创新实验实践内容（预先作用原理）、突出团队协作（分割原理、组合原理）、优化考核模式（多维原理）对《数字信号处理》课程的实验教学模式进行了探讨。

黄晶[5]等人（2019）用TRIZ理论的多用性原理、抽取原理、分割与组合原理、动态特性原理对《高等数学》教学进行改革，激发了学生的学习兴趣与提高了学习成绩。

李世巍[6]（2019）将TRIZ理论中的系统裁剪法、分割原理以及多用性原理融入高等数学课程教学中，提升了《高等数学》课程的教学效果。

刘萍[7]（2020）探索了基于TRIZ创新理论的《C语言程序设计》课程的雨课堂教学设计，教学实验证明：采用基于TRIZ创新理论设计的课前、课上、课后的雨课堂教学方式的班级的成绩优秀率、良好率、及格率、平均分、学习成果的课程达成度明显高于对照班级。

宋存米[8]（2020）应用TRIZ理论进行《C语言程序设计》课程教学改革，构建了C语言课程复杂度模型，实践证明：TRIZ理论用于教学改革是科学的、有效的。

梁娟[9]等人（2021）将TRIZ理论引入《数据库原理及应用》课程教学改革中，用预先作用原理、加强有效作用原理、反向作用原理、组合和重力补偿原理以及反馈原理等开展课堂教学，有效提高了本科课堂占课比。

郜海超[10]（2021）提出了以TRIZ理论为导向的《三维机械设计》课程改革策略：把TRIZ理论引入课程教学中，结合实物展示给学生，让学生借助TRIZ理论的40个创新原理、39个通用参数对实物进行创新设计。

武继江[11]（2022）：在《大学物理》课程教学中探索了将TRIZ理论中的40个发明原理融入课程教学内容。实践证明：这样做不仅有助于于学生理解和掌握这40个发明原理，还丰富了课程教学内容、激发了学生的学习兴趣、有效提升了学生的创新意识和创新能力。

赵佰亭[12]等人（2021）将TRIZ理论融入课程思政体系中：将课程思政系统从空间功能上分为5个子系统;确定了14个描述课程思政的系统参数，包括：思政课程观、专业课程观、思政目标、专业目标、思政内容、专业内容、思政结构、专业结构、思政活动方式、专业活动方式、思政时间、课程时间、授课对象、授课主体;对矛盾参数进行量化并建立了适配课程思政系统的TRIZ矛盾矩阵表。

郭宇刚[13]（2020）用IFR并结合40个发明原理进行微课设计，用功能分析进行教学内容设计，用九屏幕法对相关微课发展的资源进行分析，可清晰地看出微课资源的先进性，在ARIZ中用知识库作为冲突的消除有效支持。前期用九屏幕分析法确定微课方向，探究性微课以IFR最终理想解为重要分析方法，用小人法和金鱼法等创新思维设计教学过程，用物理矛盾和技术矛盾分析和解决问题，用因果链和九屏幕法寻找微课资源开发的资源，用40个发明原理设计不同类型的微课资源。

第2类：将TRIZ理论应用于创新创业教育中

罗登来[14]（2019）据TRIZ理论中的组合原则、反向联系原则、分割原则及廉价替代原则提出高校创新创业教育的改革路径为：通过组合原则培养学生行动能力;通过反向联系原则培养学生的创新能力;通过分割原则完善高校的培养方式;通过廉价替代原则降低创业成本。

张淑华[15]等人（2019）提出了TRIZ理论与我国创新创业教育的结合是一种跨专业、跨领域且多元化、多维度的深层融合，将更有助于高校创新教育培养体系的构建与实践。

焦连志[16]等人（2022）将TRIZ理念融入到大学生创新创业教育体系中，证实这样做有助于创新型人才的培养。

隋荣娟[17]等人（2022）以TRIZ理论为主线，构建了“三层次、三阶段、三融合”的创新教育体系，把创新教育融入人才培养各个环节，提高学生参与创新实践的积极性和创新能力。

魏鹏[18]（2022）以厦门理工学院为案例介绍了TRIZ在高校创新教育中的探索与实践。提出在高校开展创新方法教育应注意使创新方法教育的阶段性与高校自身定位相结合，重点培养学生的创新思维，提高学生的创新实践能力。

第3类：将TRIZ理论应用于学科专业建设中

郁佳佳[19]等人（2019）将TRIZ理论的动态化原理、预先作用原理、多维化原理融入到自动化专业的实践教学体系的建设中，探讨了在自动化专业课程考核、教学内容更新、专业教师培训、学生创新实践等各方面的改革举措。

黄文静[2]等人（2021）从打造高水平结构化师资队伍、构建科学分类的课程体系、开发面向企业真实生产环境的教学模块、教学内容融合TRIZ理论以及创新实践活动等五个方面探索了在电气自动化技术专业中如何将TRIZ创新方法融入教学，从而培养学生的精益求精的工匠精神、职业领域的精湛技艺、批判性思维能力以及较强的创新能力。

李雪[20]等人（2021）提出了基于TRIZ创新理论的“六位一体”教学创新团队建设方案：从理论建设、课程建设、竞赛建设、平台建设、实践基地，实验中心教学设备高效用6个方面，提高教学效果。

夏林中[21]等人（2021）总结了一套融合TRIZ理论中的创新原理的基于工作过程系统化方法的专业课程开发路径，为培养“技术技能型创新人才”提供支撑和参考依据。

第4类：将TRIZ理论应用于学校管理领域中

张东生[22]等人（2020）基于引文分析和共引分析理论，运用CiteSpace工具软件对WOS和CNKI数据库的相关文献进行聚类，对比分析国内外TRIZ理论在管理领域的研究表明：国外更重视团队合作和应用研究，国内更侧重理论的阐述和引申;知识管理和冲突矩阵是TRIZ在管理领域的研究热点。

李娜[23]（2020）探究了适用于教育领域的TRIZ理论。以TRIZ理论为工具提出了改进传统教育管理模式的具体思路。

刘树龙[24]等人（2020）分析了我国高校教育管理在创新发展中面临着诸多困境，概括了TRIZ理论的基本内容，并从高校创新教育发展目标出发，提出了高校教育管理的优化路径。

林雪玉[25]（2020）认为TRIZ理论是解决教育管理问题、提升管理质量与效率的重要途径与策略，在构建管理制度的过程中高校应以TRIZ理论的准则和分析方法作为规章制度的制定依据。建议高校在推广和应用TRIZ理论的过程中加强对管理者意识与能力的培训力度，推进基于TRIZ理论的教育管理层面的创新进程。认为在教育管理层面上，TRIZ理论能将系统化的知识体系渗透到管理者的管理理念中，使其通过TRIZ理论的应用经验与管理模式推动学生的全面发展。建议在实际的教育管理过程中管理者构建基于TRIZ理论的管理体系，将专业教师、课程体系的教育改革与管理结构、教学方法的变革相结合，实现对教育管理的整合化与现代化的教育目标。

综上所述，当前的相关文献虽然数量不多且占比很低，虽然有的文献只是蜻蜓点水般地介绍了融入TRIZ理论的思路或案例，但涉及到的知识点几乎覆盖了90%的TRIZ理论内容，为后续深入研究指明了方向。鉴于管理问题比技术问题涉及更多的主观影响因素，这是管理系统与技术系统典型的异质性特征;技术领域的发明原理等创新方法不能完全生搬硬套到管理领域中，增加了研究的难度和复杂度;因此，当前TRIZ理论在管理领域尤其是在高校的教育教学管理中的应用研究成果少，但对管理体系改革与创新有重大的启发价值。

三 基于TRIZ理论的高校教育教学管理方面的研究创新

（一）五级制学习复杂度模型

宋存米[8]将学习C语言课程的学习复杂度定义为完成学习内容所需要的工作量，认为学习复杂度与学习内容的难易程度与复杂程度正相关;参照“算法+数据结构=程序”公式得出学习C语言程序设计的复杂度包括“算法复杂度”和“数据结构复杂度”，在C语言中，算法的复杂度与控制结构相关，可分为简单控制结构、低复杂度控制结构、高复杂度控制结构3个级别;数据结构的复杂度与数据类型相关，可分为简单、低复杂度、高复杂度3个级别;C语言课程的学习复杂度共分九级，即简单数据类型简单控制结构→简单数据类型低复杂度控制结构→……→高复杂度数据类型高复杂度控制结构，学习复杂度呈递增态势，所需要的学习时间和训练次数呈线性增长。

上述研究成果存在两个美中不足之处：①论文题目和文中多处标题说的是“课程复杂度”，但正文中却多次描述为“学习复杂度”，容易造成误解。②将C语言课程的学习复杂度共分九级（算法复杂度有3个级别，数据结构有3个级别，3×3=9，共9个排列组合级别），然而，“简单数据类型低复杂度控制结构”和“低复杂度数据类型简单控制结构”的复杂度是几乎是同等的;同理，“简单数据类型高复杂度控制结构”和“高复杂度数据类型简单控制结构”的复杂度也几乎是同等的;所以江学习复杂度细分为九个级别是不妥当的。

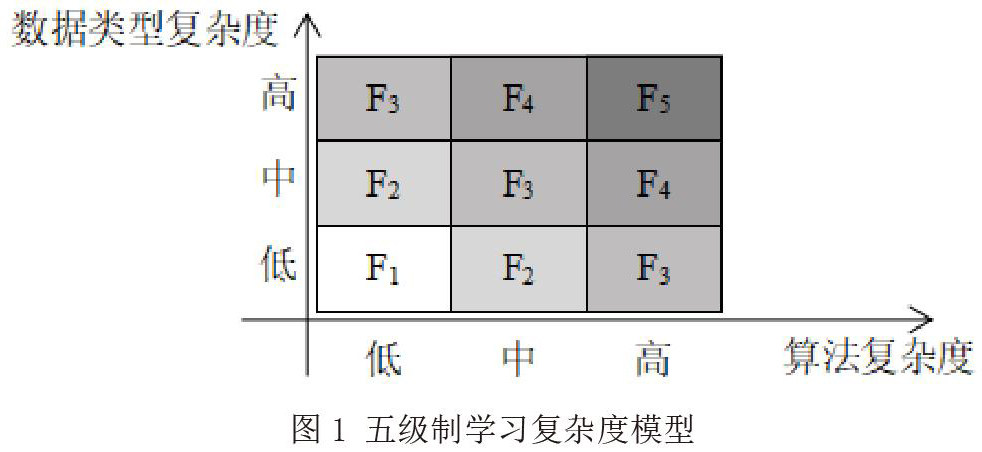
为便于理解学习复杂度模型，本文在宋存米[8]的研究成果的基础上提出一种“五级制学习复杂度模型”。该模型由横坐标（算法复杂度，分高中低3个等级）和纵坐标（数据类型复杂度，分高中低3个等级）和第一象限的九宫格表组成;在九宫格中F1～F5代表着不同的复杂度系数，右下脚标数字越大则表示复杂度系数越大，即：直观表现为复杂度系数越大则填充色越黑。

F1级别的学习复杂度系数为：0.6，设在某份试卷中，对应的题量为T1。

F2级别的学习复杂度系数为：0.7，设在某份试卷中，对应的题量为T2。

F3级别的学习复杂度系数为：0.8，设在某份试卷中，对应的题量为T3。

F4级别的学习复杂度系数为：0.9，设在某份试卷中，对应的题量为T4。

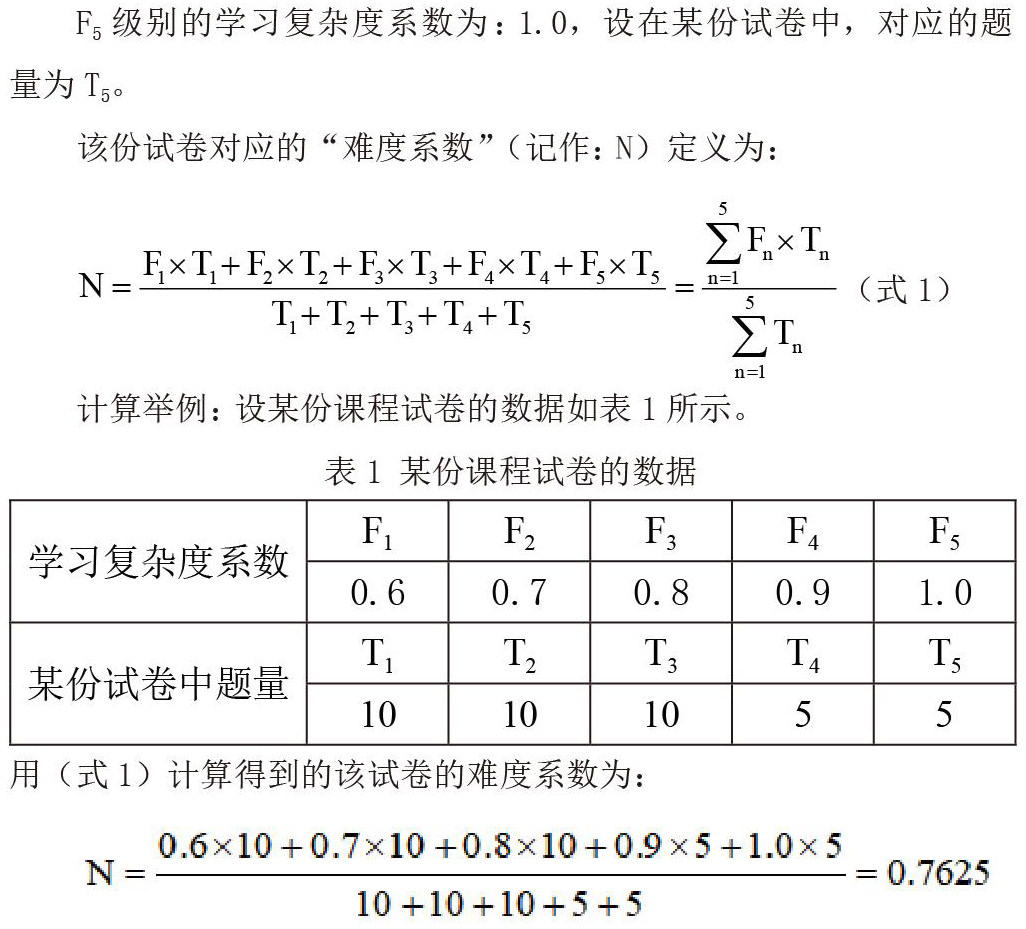
F5级别的学习复杂度系数为：1.0，设在某份试卷中，对应的题量为T5。

该份试卷对应的“难度系数”（记作：N）定义为：

计算举例：设某份课程试卷的数据如表1所示。

用（式1）计算得到的该试卷的难度系数为：

边界值分析：当试卷中全为F1等级的题目时，其难度系数取最小值：0.6;当试卷中全为F5等级的题目时，其难度系数取最大值：1.0;所以，试卷的难度系数的取值范围是[0.6，1.0]。

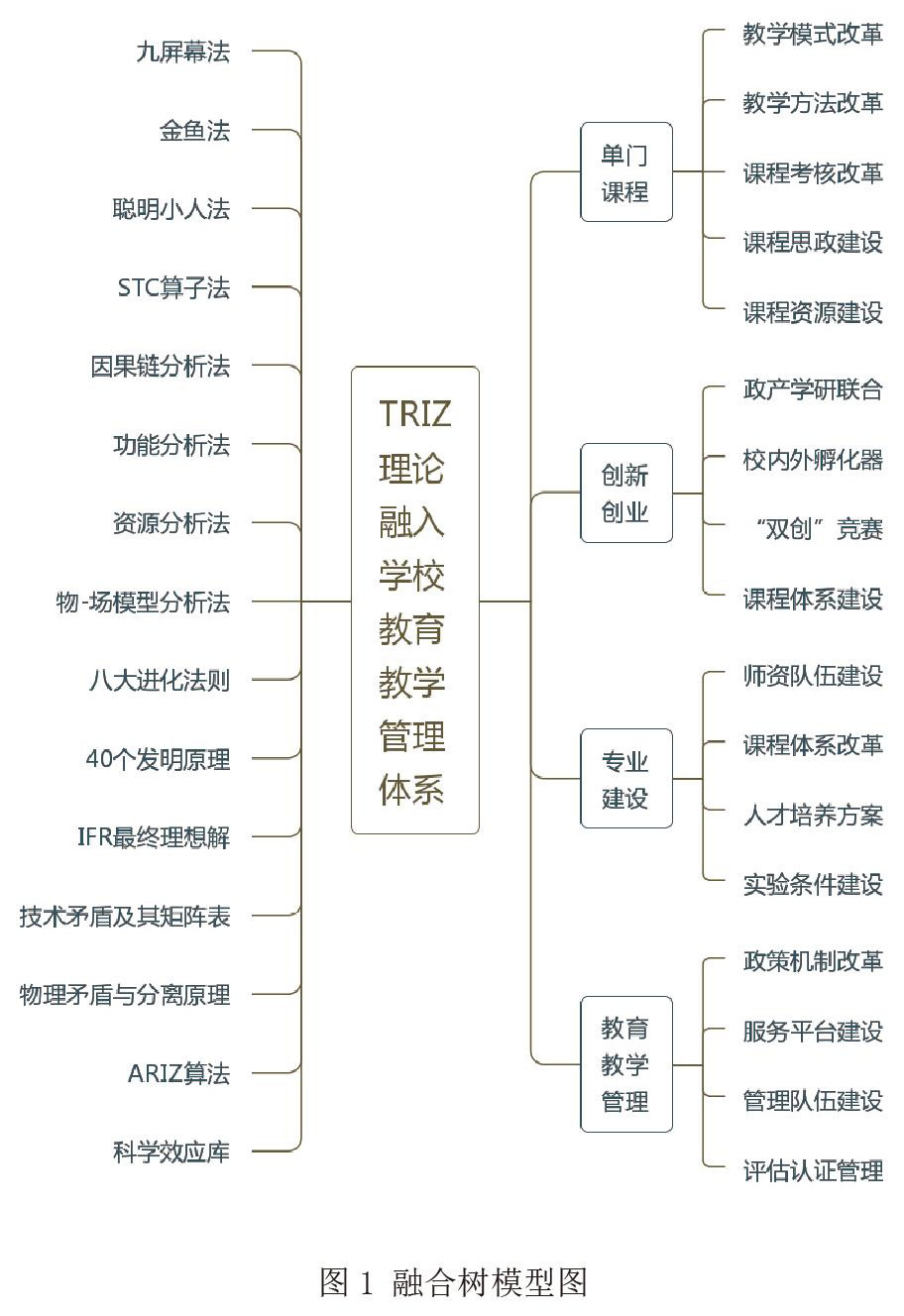
（二）教育教学管理与TRIZ理论的融合树模型

为便于日后解决学校教育教学管理问题，提出融合树模型：在图1中，左侧是融合时关联的TRIZ理论中的知识点（如九屏幕法、金鱼法、STC算子法，等常用的、成熟的创新方法或工具），右侧是TRIZ理论的融入场景或切入点（如某门课程的教学模式改革、创新创业的政产学联合改革，专业建设的师资队伍建设，等）。当我们遇到管理问题时，可以快速地从模型中寻找到创新方法或工具。

参考文献：

[1]孙晓，乔峰，李振伟，等.《电力系统自动化》教学中TRIZ创新方法探讨[J].中国电力教育，2019（11）：83-84.

[2]黄文静，张茜，李俊婷.TRIZ理论融入电气自动化技术专业教育的应用研究[J].现代制造技术与装备，2021，57（11）：219-221.

[3]朱妍雯，王亚楠.TRIZ理论在电工学课程教学中的应用[J].创新创业理论研究与实践，2019，2（07）：45-46.

[4]郁佳佳，左梅.基于TRIZ创新理论的《信号与系统》课程教学模式探索[J].教育现代化，2019，6（18）：68-69.

[5]黄晶，雷靳灿，陶科.基于TRIZ理论高等数学教学改革探索[J].科教文汇（下旬刊），2019（04）：70-71.

[6]李世巍.基于TRIZ理论的高等数学课程教学效果提升研究[J].教育现代化，2019，6（93）：147-148.

[7]刘萍.基于TRIZ创新理论的雨课堂设计与实践——以《C语言程序设计》为例[J].教育教学论坛，2020（12）：200-201.

[8]宋存米.基于TRIZ理论构建C语言课程复杂度模型[J].黑河学院学报，2020，11（03）：9-11.

[9]梁娟，吴媛，刘丹，等.基于TRIZ理论的“数据库原理及应用”课程教学研究与实践[J].无线互联科技，2021，18（04）：130-131.

[10]郜海超.以TRIZ理论为导向的“三维机械设计”课程改革探究[J].南方农机，2021，52（01）：137-138.

[11]武继江.TRIZ的40个发明原理在大学物理课程中的体现[J].创新创业理论研究与实践，2022，5（03）：151-153.

[12]赵佰亭，祝龙记，贾晓芬.TRIZ矛盾理论下的课程思政体系构建——以“单片机及接口技术”课程教学为例[J].安徽理工大学学报（社会科学版），2021，23（05）：90-95.

[13]郭宇刚，赵微，张锐.创新方法驱动下的教育资源开发研究[J].创新创业理论研究与实践，2020，3（12）：12-14.

[14]罗登来.TRIZ理论对大学生创新创业能力的培养及启示探索[J].黑河学院学报，2019，10（03）：28-29.

[15]张淑华，王霞，王泽鹏，等.基于TRIZ理论的高校创新教育培养体系构建与实践[J].山东教育（高教），2019（Z1）：109-112.

[16]焦连志，黄晓萍，毛世阳.TRIZ理论对高校大学生创新思维与能力培养的启示[J].科技创业月刊，2022，35（01）：150-153.

[17]隋荣娟，张洪丽，刘海燕.基于TRIZ理论的应用型高校创新教育教学体系[J].创新创业理论研究与实践，2022，5（08）：1-3.

[18]魏鹏.创新方法（TRIZ）教育在高校创新教育中的探索与实践[J].珠江水运，2022（13）：70-72.

[19]郁佳佳，左梅.浅析TRIZ理论在独立学院自动化专业实践教学体系中的应用[J].教育现代化，2019，6（61）：114-115.

[20]李雪，李胜利，郭菁，等.基于TRIZ理论的高校教学团队的建设与应用探讨[J].农业技术与装备，2021（10）：125-126.

[21]夏林中，龚爱平，陈煜.融合TRIZ创新原理的专业课程体系及课程开发路径探析[J].高教学刊，2021，7（20）：52-56.

[22]张东生，王文福，孙建广.管理视域下TRIZ理论研究趋势探析[J].当代经济管理，2020，42（01）：14-21.

[23]李娜.基于TRIZ理论的高校教育管理工作的创新思路[J].山东农业工程学院学报，2020，37（04）：117-119.

[24]刘树龙，闫萍，宋运贤，等.基于TRIZ理论的转型时期高校教育管理的优化路径[J].普洱学院学报，2020，36（06）：85-87.

[25]林雪玉.基于TRIZ理论的高校教育管理工作的创新思路[J].山东农业工程学院学报，2020，37（06）：162-163+171.

课题项目：本文是广东省高等教育学会“十四五”规划2021年高等教育研究课题——防疫背景下高校在线教学模式及效果评价研究（21GYB110）、2021年珠海市哲学社会科学规划课题——基于TRIZ的高校教学管理问题的解决理论研究（2021GJ189）、2021年北京理工大学珠海学院“线上线下混合式一流课程”项目——《程序设计基础及应用》（YLJC2021005）的研究成果。

作者简介：黄振永，1979年4月出生，男，江苏徐州人，硕士，讲师，北京理工大学珠海学院信息学院，专任教师，研究方向：光学工程和TRIZ理论