打开文本图片集

【摘要】数学史融入课堂为新课标背景下落实学生数学核心素养的培养与发展起到积极的促进作用。以“分数除法解决问题”为例，设计数学史融入小学数学的教学案例，在此基础上探究数学史融入数学教学的价值，关注学生核心素养的培养，促进学生的全面发展。

【关键词】数学史;分数除法解决问题;教学设计

《义务教育数学课程标准（2022版）》充分肯定了数学文化在数学教学中的作用，明确指出“数学课程承载着思想和文化，是人类文明的重要组成部分。在教学中应展现数学发展史中伟大的数学家，特别是中国古代与近现代著名数学家，以及他们的数学成果在人类文明发展中的作用，增强学生的爱国情怀和民族自豪感。”[1]新课标的颁布为课堂教学改革提出了新的挑战，而数学史作为数学文化的重要依托，具有重大的教育价值。以“分数除法解决问题”为例，进行数学史融入教学的设计探究，旨在通过恰当的数学史运用方式，发挥其育人功能。

一、背景

分数除法是数的运算中重要的一种类型，“分数除法解决问题”是“分数除法”单元的第四课时，该课时的学习可以培养学生的运算能力、问题解决能力、模型意识和应用意识。在学习“分数除法解决问题”前，学生已经学习了分数除法的计算方法和分数乘法解决问题的知识内容，对分数除法解决问题的步骤和方法有一定的认知基础。关于本课时的已有教学设计并未充分融入数学史素材，让学生感受其悠久的历史、数学的多元文化。结合以上思考，尝试数学史融入“分数除法解决问题”的教学设计，让学生认识到相关问题作为古往今来各个文明中重要的存在而具有的重要价值，感受数学与生活的联系，体悟数学与历史的联系，激发数学学习的兴趣与信心。

二、历史素材

分数除法是数学历史与发展中不可回避的议题，因此分数除法相关内容有丰富的历史素材可供选取。古代各个文明都有著作传世，特选取具有代表性的古埃及、古希腊、欧洲中世纪以及中国明代的史料，以期通过数学史融入教学发挥其教育价值。

《莱茵德数学纸草书》记载了一些有代表性的古埃及数学工作。古埃及数学的重要且有趣的特色是单位分数的广泛使用。《莱因德数学纸草书》给出了一张形如（k为从5到101的奇数）的分数分解为单位分数之和的表。埃及人对分数的运算都化作单位分数来计算，因此对分数的记法和计算都比现在复杂得多，这也妨碍了埃及数学的进一步发展。书中涉及分数除法应用的有第24题与第31题，在纸草书中均采用的假设法，与现今计算方法相比复杂得多。[2]数学史的融入在于沟通古今，让学生在感受古代先贤智慧同时自豪于自己更简洁的算法，从而树立学习数学的信心。

丢番图（Diophantus，约246-330）是古希腊的著名数学家，被誉为“代数之父”，他创建了独特的字母符号和体系，其代表著作《算术》对代数领域的发展具有重大贡献。同样有趣的是丢番图的生平。在六世纪元年前后收集的一本《希腊诗选》里，有一首恰好是丢番图的墓志铭，正好可以用分数除法应用中的解方程来解答问题。[3]本文选取丢番图的墓志铭作为数学史材料融入教学中，意在放眼世界，感受不同文明中无处不在的数学思维，建构数学与历史、文学、诗歌等多元交织的桥梁，培养学生以数学的眼光和开阔的视角看世界。

《计算之书》是意大利数学家斐波那契（Leonardo Fibonacci，约1170-1250）的重要数学著作之一，内容涉及算术、代数、几何和问题解决等在13世纪广为人知的数学知识，其理论基础是欧几里得的数学。书中数学问题的东方背景特别引人注目，斐波那契《计算之书》对于揭示文艺复兴近代数学的东方来源和中国影响，具有特殊的意义。[4]本文选取书中第十二章第三部分的一系列的求树高的历史名题，均涉及分数除法解决问题，斐波那契将其命名为“树问题”。借用数学史材料，激发学生的探究欲望，其中求树高问题链的设计便于学生在熟悉情境中迁移应用已知知识，提高学生的迁移类推能力。

中国明代程大位（1533-1606）所著《算法统宗》集珠算之大成，是我国珠算史上的一个里程碑。它的成书及其广泛流传，标志着由筹算到珠算这一转变的完成。[5]书中“绩麻分布”篇有关于分数除法应用的诗歌，是帮助解决合理分布匹的问题。[6]本文选取此诗歌作为数学史素材，让学生体会古代数学与日常生活的紧密联系，感受数学的有用性和实用性，激发学习动机。

三、教学设计

1.教学目标

（1）学会分数除法解决实际问题的解答方法，会根据关键信息列出数量关系，会熟练地列算式或列方程解答。

（2）经历分析、判断和推理的过程，学会用线段图分析数量关系，理解并感悟数形结合和方程思想，提高分析问题和解决问题的能力。

（3）感受数学与生活的联系，在历史名题的探究过程中获得成功体验，树立数学学习的信心与保持数学学习的兴趣。

2.教学过程设计

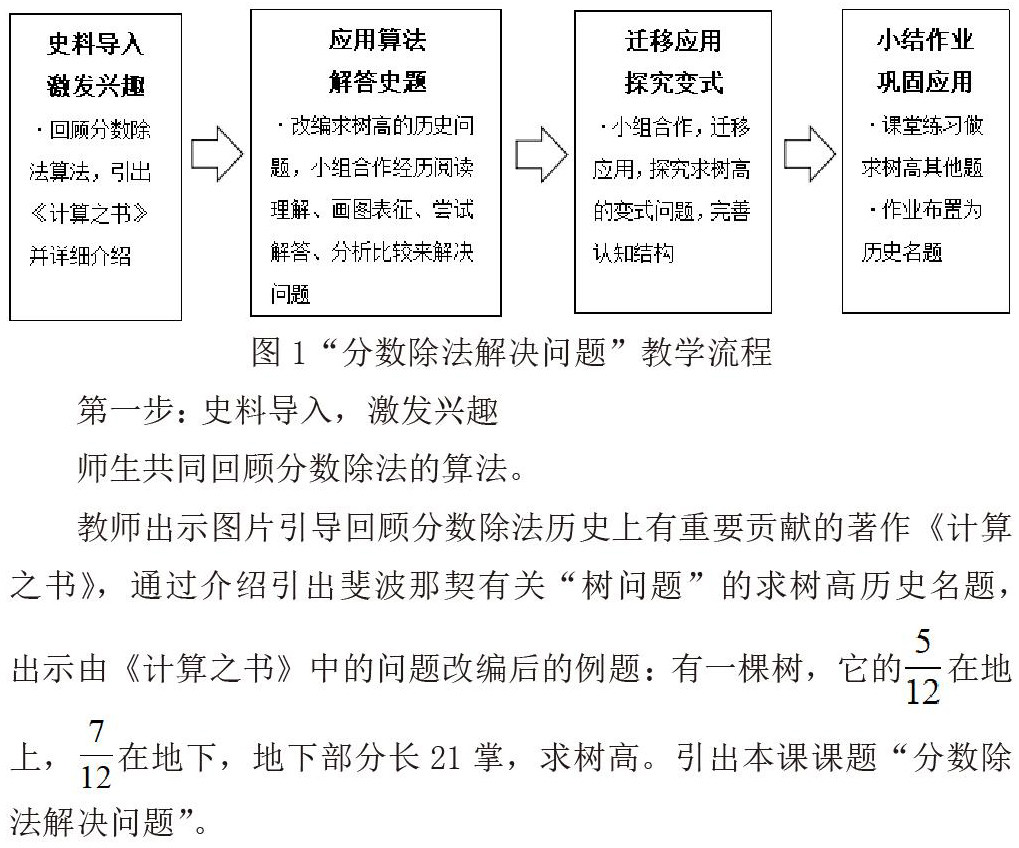
“分数除法解决问题”属于问题解决教学，具体教学流程如图所示：

③丢番图的墓志铭如下，试求他活了多少岁？

“坟墓里边安葬着丢番图，

多么让人惊讶，

他所经历的道路忠实地记录如下：

上帝给予的童年占六分之一

又过了十二分之一，两颊长须，

再过七分之一，点燃起婚礼的蜡烛。

五年之后天赐贵子，

可怜迟到的宁馨儿，

享年仅及父亲的一半，便进入冰冷的墓。

悲伤只有用整数的研究去弥补，

又过了四年，他也走完了人生的旅途。”

④“赵嫂自言快绩麻，李宅张家雇了她。

李宅六斤十二两，二斤四两是张家。

共织七十二尺布，二人分布闹喧哗。

借问乡中能算士.如何分得无差？”——《算法统宗》（注：古时一斤等于十六两）

（设计意图：课堂练习是巩固新知的重要手段，此环节继续选用《计算之书》中求树高的问题链，以同一问题情境贯穿整节课，体会古代数学与日常生活的紧密联系，现代数学依托古代数学而发展，感受古代先贤的数学智慧，同时也为以后“比例”的学习打下基础。在作业布置环节，选取其他数学名著上的历史名题，意在放眼世界，感受不同文明中无处不在的数学思维，建构数学与历史、文学、诗歌等多元交织的桥梁，培养学生以数学的眼光和开阔的视角看世界。）

3.数学史的运用方式

在教学的各个环节，分别使用“附加式”、“复制式”和“顺应式”把数学史有机融入教学之中，真正环环相扣地将数学史融入在学生的学习之中，以促进学生的最大发展。

在导入环节采用“附加式”介绍欧洲中世纪数学著作《计算之书》，因此作为本课伊始的导入材料既不陌生，也为“树问题”问题链的设置介绍背景，为解决求树高的问题引出“分数除法解决问题”的课题，吸引学生的注意力并激发探究欲望。

在探索新知环节采用“顺应式”对求树高问题进行改编，添加干扰项，意在与教材内容有机整合，培养学生解决问题时的提取有效信息能力。求树高这个具体情境与学生生活紧密联系也是选取此历史名题的重要原因之一。

在探究问题变式环节依旧采用“顺应式”对求树高问题进行改编，题意不变仅改变数值，此改变是为了简化学生的计算，方便使用线段图直观反映数量关系。

在课堂练习环节直接“复制”求树高的其他历史名题，利于学生在相同情境下迁移应用知识，与前两环节共同完整地呈现了“树问题”的一系列历史问题，学生在巩固分数除法解决问题的基础上，加深对斐波那契《计算之书》中的著名历史问题——“树问题”的了解，由于斐波那契是用比例来解决问题，同时为以后“比例”的学习奠定基础。

在作业布置环节采用“复制式”呈现历史问题，体会古代数学与日常生活的紧密联系，现代数学依托古代数学而发展，感受古代先贤的数学智慧，同时在解决历史名题之后树立数学学习的信心。

四、数学史的价值

数学史融入教学加深学生对知识的理解。《计算之书》中的一系列“树问题”贯穿整个课时，为“分数除法解决问题”的探究活动的设计提供了具体情境。一方面，让学生体会学习分数除法解决问题的必要性;另一方面，学生在多维发散思路而寻求不同算法的过程中，积累数学活动经验，迁移与应用相关知识，改善学生对数学知识理解的困境。

数学史融入教学促进学生能力的发展。一方面，“树问题”相关历史素材融入教学提供了相同情境，对新知的探究环环相扣，而例题中仅有数据改变，便于学生在相同情境中迁移知识，培养学生的迁移与类推的能力，同时课堂练习中各个历史名题也培养学生的阅读理解与分析问题的能力，真正实现了促进学生能力发展的目标。另一方面，各个文明中数学史素材将数学中有趣的一面展示给了学生，沟通了数学与历史、文学、诗歌等多元交织的桥梁，展现了数学之美，提升学生的美学鉴赏能力，同时丰富学生的文化涵养。

数学史融入教学发挥数学的德育功效。数学史的融入让学生感受“分数除法解决问题”在历史中的价值，体会到数学学习的历史相似性，今天所遇到的问题古代数学家也遇到过，并且自己成功解决问题获得的成就感就像自己也是一位优秀的数学家，提升数学学习的信心以及遇到困难努力解决的决心。同时，让学生体悟古代数学家的理性精神，汲取榜样的力量，锻炼坚强的意志，养成良好的心理品质，达到德育的功效。

总之，数学史的融入具有重大价值，对学生的知识理解、能力发展和德育培养都起到促进作用。同时以独特的课堂教学视角来落实学生数学核心素养的培养与发展，聚焦数学学科的核心价值。

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准[M].北京：北京师范大学出版社，2022.

[2] A.B.Chace. The Rhind Mathematical Papyrus [M]. Oberlin： Mathematical Association of America， 1929.

[3]蔡天新. 数学与人类文明[M].北京：商务印书馆，2012.

[4][意]斐波那契著，纪志刚，汪晓勤等译：《计算之书》，科学出版社2008年版，第297-299页.

[5]吴文俊. 中国数学史大系——第六卷 西夏金元明[M].北京：北京师范大学出版社，1999.

[6]徐品方，徐伟.古算诗题探源[M].北京：科学出版社，2015.

基金项目：信阳师范学院研究生科研创新基金资助

作者信息：张小艺，1992年3月，女，河南平顶山人，信阳师范学院小学教育专业硕士研究生在读，主要研究方向为数学史与数学教育