打开文本图片集

【教学目标】

1、理解三角形中位线的概念，掌握它的性质，应用三角形中位线定理进行有关的证明和计算．

2、经历探索、猜想、证明的过程，进一步发展推理论证的能力．

3、能运用综合法证明三角形中位线定理，理解在证明过程中所运用的归纳、类比、转化等思想方法.

【教学重点】

掌握和运用三角形中位线定理.

【教学难点】

三角形中位线定理的相关证明.

【教学过程】

活动一：创设情境  初识定理

设计意图：

以学校劳动教育课程中的菜地分田问题作为情境，引导学生带着疑问进入新课，激发学生的好奇心与求知欲.通过小组讨论交流展示分割方案，回顾中线的性质，进而引出本节课学习主题。

课堂引入

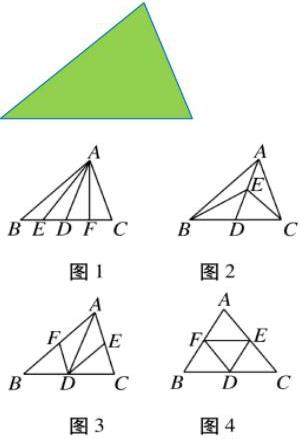
如图，学校菜地有一块三角形的试验田，准备平均分给四个班级，现征集设计方案。

要求：1.他们所分的大小相同；

2.各班所分区域美观大方。

学生活动：

1.自主设计分割方案；

2.小组交流各自的设计方案，探究其它方案；

3.以小组为单位展示分割方案.

活动评价（组内互评）：

A：能积极主动思考，并尝试用不同方法进行分割.

B：能积极主动思考，并尝试用一种方法进行分割.

C：能参与活动，并在组员的帮助下进行分割.

活动二：实验发现 归纳定理

设计意图：

通过前面的分割引导学生用自己的话描述三角形中位线，进而给出三角形的中位线的定义，既让学生得出三角形的中位线的概念，又让学生在无形中区分了三角形的中线和三角形的中位线．

证明的过程感悟三角形中位线定理与平行四边形的内在联系，既要让学生学会知识点之间的联想感悟，又要锻炼其大胆猜想，严谨论证的学习精神．

对于定理证明方法的探索是本节课的难点，采取小组合作学习与启发式教学相结合的方式展开，在学生交流讨论时充分发现和肯定学 生的思路，顺势利导，展示多种证明方法引导学生观察、分析、类比、猜想，体验知识的生成过程，使传授的数学知识成为学生自己思考获得的结果，从而抓住重点，突破难点.、

通过小组展示不同的方法，开拓学生的视野，有利于培养学生的发散思维和创新能力．

问题1：在上述方案中都用到了哪些线段？请尝试用自己的话描述.

预设学生回答：有三角形的中线，还有两边中点之间的线段.

这样的线段就是我们今天要学习的三角形的中位线.（引入课题）

定义：连接三角形两边中点的线段叫做三角形的中位线．

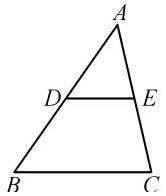
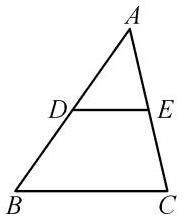
问题：2：如图，DE是△ABC的中位线，DE与BC有怎样的关系？

猜想：三角形的中位线平行于三角形的第三边且等于第三边的一半．

问题3：如何利用所学知识验证你的猜想呢？

学生活动：

1.独立思考3分钟后小组合作交流验证过程；

2.以小组为单位展示证明过程.

活动评价（组内互评）：

A：能积极主动思考，并尝试用不同方法验证猜想.

B：能积极主动思考，并尝试用一种方法验证猜想.

C：能参与活动，并在组员的帮助下验证猜想.

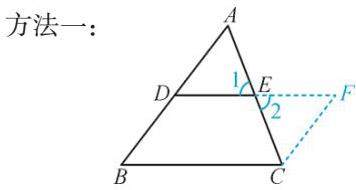
方法一：

证明：延长DE到F，使FE＝DE，连接CF.

在△ADE和△CFE中，

∵AE＝CE，∠1＝∠2，DE＝FE，

∴△ADE≌△CFE.

∴∠A＝∠ECF，AD＝CF.

∴CF∥AB.

∵BD＝AD，∴CF＝BD.

∴四边形DBCF是平行四边形．

∴DF∥BC，DF＝BC.

∴DE∥BC，DE＝BC.

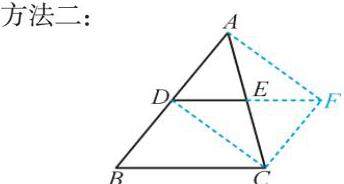
方法二：

证明：延长DE到点F，使EF＝DE，连接FC，DC，AF.

∵AE＝EC，DE＝EF，

∴四边形ADCF是平行四边形，

∴CF∥DA. CF=DA.

∵AD＝BD，

∴CF=BD.

∴四边形DBCF是平行四边形，

∴DF=BC ，DF∥BC.

又∵DE＝DF，

∴DE∥BC，且DE＝BC.

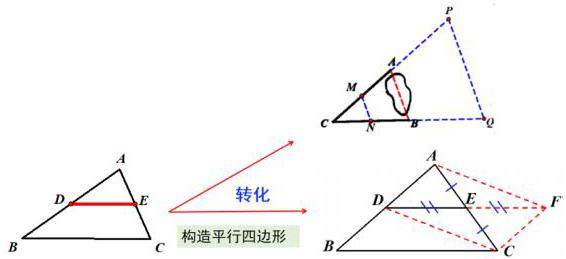
师生活动：小组展示后，教师应引导学生共同总结归纳出不同方法的本质：适当添加辅助线构造平行四边形是解决这一问题的关键．

总结：三角形的中位线定理：三角形的中位线平行于第三边，且等于第三边的一半．

图形与符号语言：

如图所示，在△ABC中，D，E分别是边AB，AC的中点，

∴DE∥BC，DE＝BC.

定理作用：①证明平行问题．②证明一条线段是另一条线段的2倍或.

活动三：牛刀小试 应用定理

设计意图：

检验学生对本节课知识的掌握程度、理解程度和运用程度．运用三角形的中位线定理解决问题，提高学生解决问题的能力.通过问题的解决，一方面用来检查学生对三角形中位线的理解、掌握和运用情况，另一方面，规范学生的解题步骤和格式.

通过老师的批改使每一个学生都能动起来，充分调动学生学习的积极性，有针对性的进行帮扶，有利于本节课目标的达成.

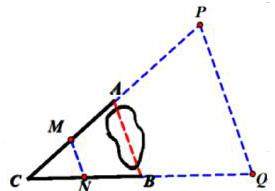
1.如图，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC.怎么测出A，B两点间的距离？依据是什么？

方法一：取AC，BC中点M，N，连接MN，根据MN=AB，测量MN可得AB的长度；

方法二：延长CA至P，使PA=AC，延长CB至Q，使QB=BC，连接PQ，根据AB=PQ，测量PQ可得AB的长度.

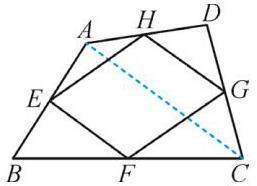
2.如图，顺次连接四边形ABCD的四条边的中点E，F，G，H，所得的四边形EFGH有什么特点？并证明．

解：四边形EFGH是平行四边形．

证明：连接AC.

∵E，F分别是AB，BC边的中点，

∴EF是△ABC的中位线．

∴EF＝AC且EF∥AC.

同理可得，GH＝AC且GH∥AC.

∴EF＝GH且EF∥GH.

∴四边形EFGH为平行四边形．

师生活动：学生进行课堂检测，完成后，教师批阅完成快的，指派优秀作业的同学成为老师批改其他同学的作业.

活动四：课堂反思 整理小结

设计意图：

注重课堂小结，激发学生参与课堂总结的主动性，为每一个学生的发展与表现创造机会.

三角形中位线定理

在△ABC中，

∵ D，E分别是边AB，AC的中点，

∴ DE∥BC，且DE=BC.

活动五：课后练习 反馈提升

设计意图：

以学生身边最为关注的劳动教育试验田的分田为背景设置开放性的作业，激发学生探索解决的欲望，进一步巩固所学知识.

学校的劳动教育实验田，是一个三角形地块，现需将此实验田分给四个班管理，请你按照如下要求设计一个分配方案：

1.四个班的管理面积相等（可以是一个完整地块也可以是多个小地块）；

2.设计美观，可搭配种植不同种类或不同颜色的植物；

3.请证明你的设计方案满足条件.