打开文本图片集

摘要：本文按照基本强迫振动的数学理论，结合塔式起重机自身结构特点和我国现行塔式起重机设计的相关规范，就目前频繁发生的强台风导致塔式起重机倒塌事件，分析塔式起重机强风风振机理，基于随机风振理论摸索新的塔式起重机非工作状态下的风荷载数学计算方法，为提高其抗风能力提供参考。

关键词：塔式起重机；台风；强迫振动；风振响应

我国每年的夏季和秋季，东南沿海地区很容易受到热带低压、热带风暴、强热带风暴、台风、强台风、超级台风等热带气旋的影响。根据基本振动理论，塔式起重机（以下称塔机）在台风风载荷下发生了强迫振动。由于自身钢结构的特殊性，在质量和受风作用特性方面，其数学计算理论也有所不同。

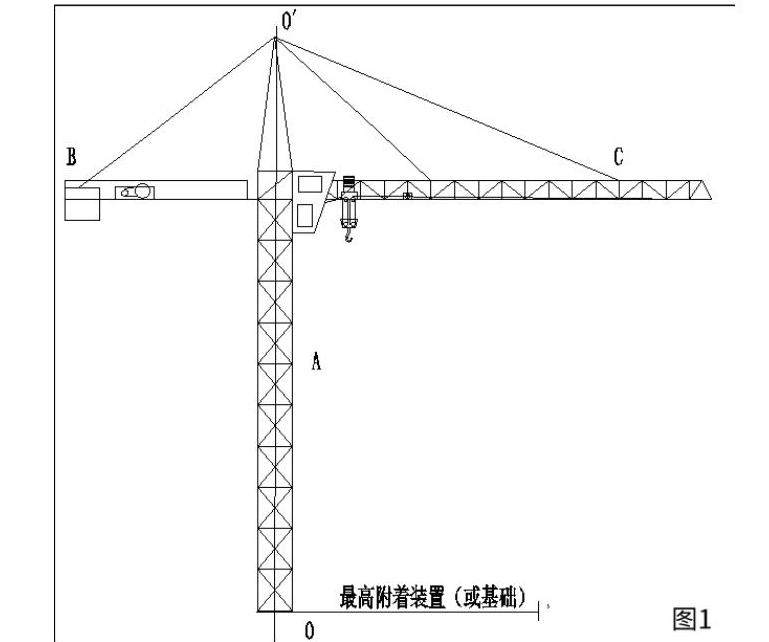
与一般高层建筑不同，塔机由于自身结构决定了它始终属于偏心振子振动类型。如图1，塔机在台风作用下，上机体（指塔机最高附着装置以上部分）作为振子振动单元包含平衡臂、工作臂及上机体塔身等，受到的不仅仅是重力，而是重力、塔身弹性回复力和风力组成的综合作用力振动体系。

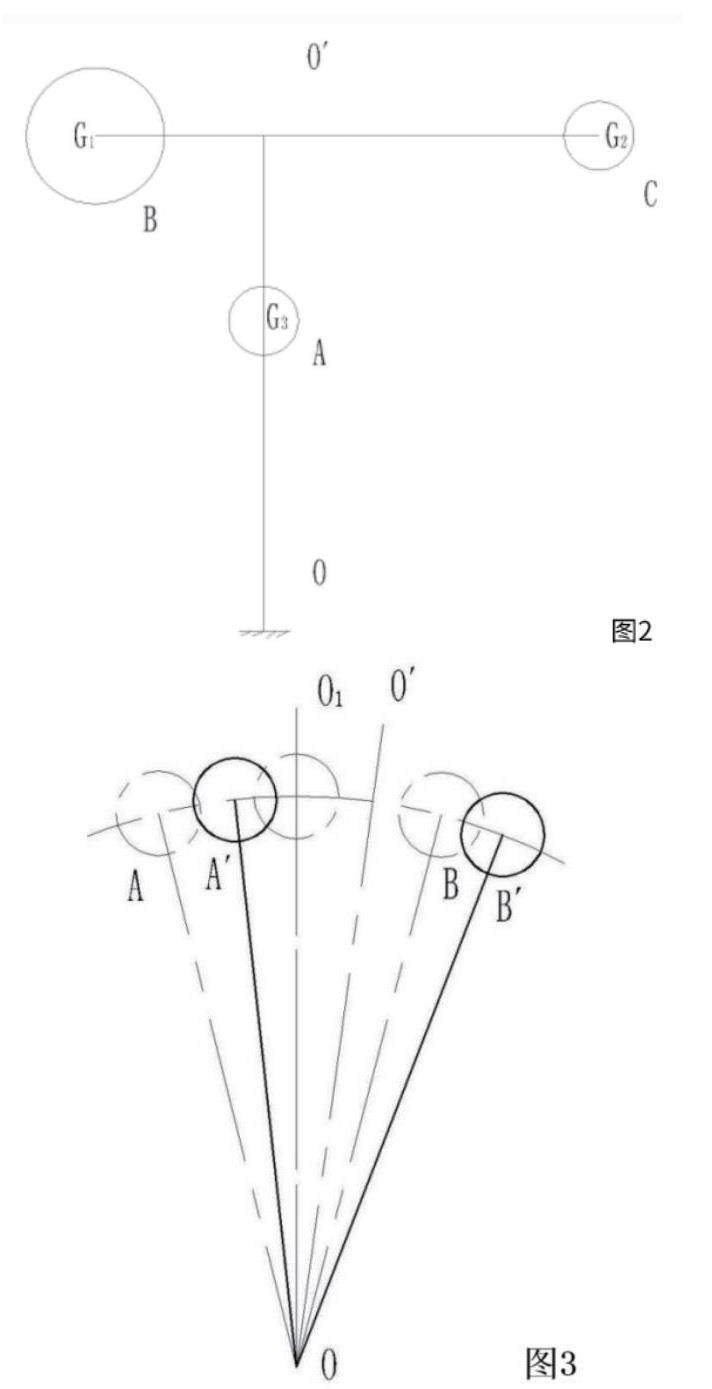
上机体主要由平衡臂、工作臂、塔身三个部分组成。如图2，其当量质量分布G1（平衡臂）、G2（工作臂）和G3（塔身）。当塔机最高附着装置未被破坏之前，塔身在该附着处可以认为是静定状态。为了方便数学建模分析其振动状态，可对该静定点以上主要质量组件进行以下数学建模：图中，弹性体1为塔机塔身作为振子的振动弹性体；弹性体2为平衡臂作为振子的振动弹性体；弹性体3和弹性体4共同为塔机工作臂振子的振动弹性体。由于这种多元振动构成的弹簧振子系统数学建模较为复杂，作进一步进行简化，把所有附着装置以上部分看成一个弹性振子，仅保留一个整体振子建立数学模型。实际上，塔机上机体重心总是偏离塔身轴线一定距离，如不计这个偏心值，简化为由一个振子（质量为G）和由塔身自身弹性构成的弹簧振子，在重力和塔身弹性体综合作下的振动如下：在只有重力或弹力做功的系统内，动能与势能互相转化时能量保持不变。但台风中的塔机风振显然不满足“只有重力或弹力做功”这个前提。风振过程中，上机体的机械能有：受到塔身标准节抗弯模量影响，弹性势能、重力势能和风荷载作用获得的动能相互转换。

如图3所示，在稳定持续风力（设为f=f1）作用下，上机体作为弹性振子实际上的振动中心会发生偏离，振动中心由原来的OO'偏移到OO´。振幅也由原来的OA、OB偏移到OA´、OB´位置。

风振过程：左来流顺风向，塔机机体不断吸收风动能，同时塔身标准节释放出弹性势能，致使动能不断获取，速度开始逐步增加；当到达平衡位置0＇（此时风力+重力分力=回弹力）时，速度到达最大，紧接着由于上机体的惯性作用，越过平衡位置，此时塔身回弹力继续增大，风力仍然作用于上机体，但由于标准节回弹力作用吸收了上机体的动能，转化成自身弹性势能，尽管风能不断在补充，上机体的动能仍不断被标准节回弹力消耗，速度逐渐降低，最后为0（B＇）；这就是持续稳定强风下的最大弯曲变形状态。当风压发生减弱，上机体回弹于逆风向风场，由于在顺风方向上储蓄了相当的弹性势能（此时风力+重力分力＜回弹力），标准节弹性势能开始释放，迫使上机体不断获取动能，速度逐渐加快，当到达平衡位置（0＇）时，速度到达最快（但远小于顺风向下的最大速度）。越过平衡位置后，上机体继续受到逆风和标准节弹性反向作用，不断消耗前面转化来的动能，速度又逐渐减慢，标准节弹性势能随之反向增加，速度减慢为0（A＇），标准节弹性势能反向最大（但远小于顺风向下的弹性势能）。

实际上，如果在稳定持续风力（设为f=f1）作用下偶尔加上一个阵风，在f＜f1时，振子振荡中心OO´会“抬头”向平衡位置偏移，这种情况是安全的。但如果在稳定持续风力作用下偶尔加上一个较大的阵风（f＞f1），且满足一个半周期时间的持续阵风，在振子回摆到最左侧时，开始以f＞f1的速度吹向振子，等振子回摆到最右侧时，阵风消失，振子会再次回摆到左侧，再来一次等大或加大的阵风，这就满足了风荷载共振条件！在一次台风的整过程，这种短时间规律阵风（指满足一个振动周期的阵风）难免存在，其破坏力最大，也是最危险的台风风况。

可以说只要物体作周期性的往复运动，就是振动。注意到有一个数学分枝叫做傅里叶积分，它可以把任何振动，分解为若干个简谐振动。根据这个描述，我们可以把台风中的塔机上机体的摇摆认为是由上机体重力与标准节组成的简谐振动和由上机体风载与标准节组成的简谐振动的叠加。

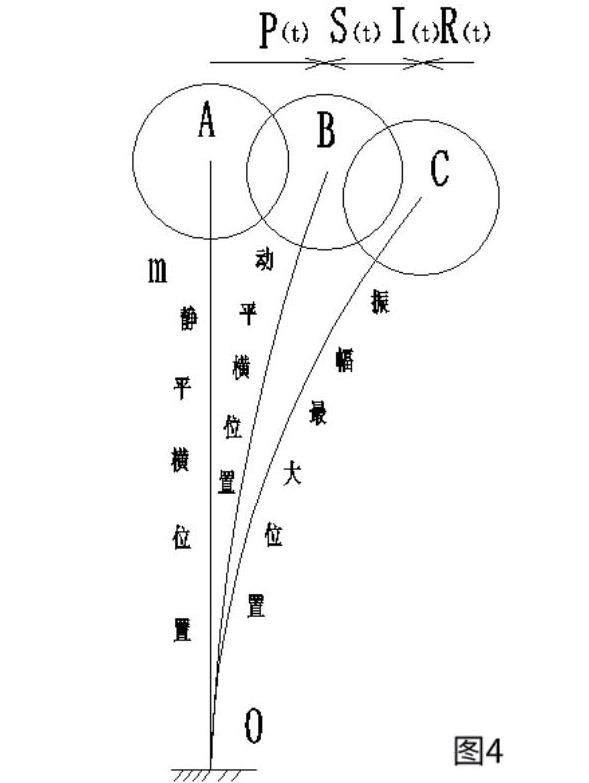
对塔机作抗台风荷载计算时，塔身部分可以把它看成单自由度结构体系。平衡臂和工作臂可以把它分别看成固定在塔身顶部的单自由度结构体系，如图4所示。它的运动计算方程分析如下：

塔机结构振动体当量质点（以下称质点）动力计算的基本未知量是上机体回转部位的位移，它是时间t的函数。为了求出动力反应，应先列出求解质点位移的方程。建立运动方程常用的方法是动静法。根据达朗贝尔原理，将惯性力假想地作用在质点m上，在振动的每一瞬时，惯性力与结构受到的动荷载、约束反力等在形式上组成一平衡力系（动平衡），于是就可以利用静力学中的方法建立运动方程。

在振动的任一时刻t取质点m为隔离体作用在质点上的力有：（1）重力W，由于受迫振动质点的重力与运动方向几乎垂直，忽略重力对本振动体系贡献；（2）风荷载P（t）；（3）塔身钢结构弹性恢复力S（t）。它是由于塔身标准节的弹性变形而施加于质点的力，它的大小与质点m的位移成正比，但方向相反，即S（t）=-k[∆+y（t）]；式中k为塔身的刚度系数，其意义相当于塔身的抗弯模量W；∆为平均风作用下质点偏离静平衡位置的水平位移；y（t）为脉动风（或阵风）作用下质点受迫振动的位移；（4）惯性力I（t）。其大小为质点质量m与质点加速度的乘积，方向与加速度的方向相反，即；惯性力沿动位移y（t）的正向作用。（5）由于风介质本身的粘性具有的阻尼力R（t）。关于阻尼力的理论有多种，这里采用计算较简单的粘滞阻尼理论。它假定阻尼力R（t）与质点速度成正比，方向与速度的方向相反，即 ，当然，相对质点的质点速度，风速明显大得多，因此可认为R（t）=－cVmax； c称为粘滞阻尼系数。考虑质点m的动力平衡ΣY=0，应有；即：

这就是质点受迫振动的连续化一维运动微分方程。上述方法是直接利用达朗贝尔原理建立质点m在任一瞬时的强风作用下塔机受迫振动的动力平衡方程。引入标准节抗弯模量，令k=EI（z），则转化为：，其中EI（z）是z高处标准节的刚度值，这里的风速包括了平均风速和脉动风速，它服从零均值的平稳高斯分布。

一般而言，根据《建筑结构载荷规范》（GB 50009-2012 ），风振计算有以下几个组成部分：

1.基本风速

由于塔机结构从塔机受力主体形态和非工作状态下类似于工作状态下大跨越高塔，根据现行《高耸结构设计规范》（GB 50135-2019）4.2.15之规定执行，设计最大风速按50年重现期确定，应按当地气象台、站的10min时距平均年最大风速做样本，宜采用极值I型分布作为概率模型。且考虑在建的建筑物阻挡作用，宜参考该条第三点“位于山地上的高塔的最大设计风速，应按附近平地的统计值提高10%选用”。

2.风振系数

受建筑物影响的塔机，其横风振受决于建筑物的漩涡脱落形成的风振，而建筑物迎风面千变万化，所形成的漩涡脱落也千变万化，正如《高耸结构设计规范》4.2.9所述，规范列出的公式（4.2.9）是根据荷载规范针对第一振型影响的结构，随着计算机的普及应用，只考虑第一振型影响已不能满足要求，而且也不必要，可根据基本原理考虑多振型影响进行电算。

3.横风共振

在设计中，往往关心钢结构使用期间可能遇上的最大风速问题，也就是极值风速问题，其实通过大量观察发现，台风风体是大量的顺风加上阵风混交在一起的混合体，风场相对由长时间的稳定加上短时间内的不稳定构成，风场经过的路线也是大体的固定加上小范围的旋转不固定。因此在稻田里会出现倒伏一致性路线和旋转圈，在树的顶端会出现成片摆倒和下旋或上旋现象，没有规律可循。

结束语

综上所述，对于塔机而言，它遇到的实际最大风作用可能是平稳风最大风速，也可能是阵风最大风速，更有可能是平稳风加上阵风的最大风速。但可以肯定的是风场是连续的，至少在足够短的时间内是连续的。当然它不可能按照某一个分布理论公式去存在，但应用某一个分布理论去研究是可以去涵盖它所造成的风振响应，这就是我们希望得到的结果，也是提高塔机抗风设计的有效手段。

参考文献

[1]张福寿，王国砚.框剪结构简化振型及在高层建筑风振计算中的应用[J].结构工程师，2020.36（2）.130-136.

[2]原迁，张德凯.大跨越输电塔线体系风振响应及风振系数分析[J].山西建筑，2021.47（6）.34-38.

[3]GB/T 3811-2008 起重机械设计规范[S].

[4]GB/T13752-2017 塔式起重机设计规范[S].

[5]GB 50009-2012 建筑结构荷载规范 [S].

[6]GB 50135-2019 高耸结构设计标准 [S].

[7]武岳，孙 瑛，郑朝荣，孙晓颖.风工程与结构抗风设计[M].哈尔滨工业大学出版社，2019.79-81.

[8]张相庭.结构风工程[M].中国建筑工业出版社，2006.120.

作者简介：黄仕修（1973～），男，学士，机械工程师，起重机械检验师，主要从事机电类特种设备定期和监督检验研究工作。