打开文本图片集

摘要：向量法是连接几何知识和代数知识的桥梁，应用于解三角形中可以培养学生从多个角度解决数学问题的能力，提高学生的数学思维。本文主要分析了高中数学“解三角形”的关键方法，从了解向量与解三角形的基本关系、构建合作学习小组开展教学对高中数学解三角形的具体方法展开了探讨，重点剖析了利用向量法解三角形的内容。

关键词：高中数学；解三角形；教学方法

引言：

高中数学教材中包含几何知识和代数知识两大内容，为提高学生解决问题的能力，培养学生从多个角度思考问题的思维，需要引入数形结合的问题，掌握通过代数方法解决几何问题，或者通过几何方法解决代数问题的能力。解三角形是对任意三角形边角关系的探索，在一些测量和几何计算中具有实际的应用意义，其关键在于能否抓住解三角形的知识和方法。

一、高中数学“解三角形”的关键方法

解三角形一向是高考热门考点，也会高中数学教学的重点和难点。结合教材内容来看，三角形串联起的高中知识点比较多，包括三角函数、向量、不等式的综合应用等。想要掌握解三角形的正确方法，首先要明确三角形的基本特征和具体方法的各自特征。题型的不同，对解三角形相关知识点考察的重心和重点问题也不一样。对于刚升入高中的学生来说，锻炼学生的数学逻辑思维，培养数学素养显得尤为重要。向量的概念相对抽象，公式比较独立，但是向量具有几何形式和代数形式双重身份，可以将向量的坐标公式和非坐标公式进行结合，成为实现数形转换，连接代数知识点和几何知识点的关键桥梁。

二、利用向量解三角形的实践教学方法

（一）了解向量与解三角形的基本关系

利用向量法研究三角形的性质是高一数学的教学难点，也是重点。高中数学知识具有系统性、整体性的特征，在数学研究和数学教学中经常会出现对已经研究过的对象使用新的数学工具、数学思维和数学方法重新再研究的情况，这种形式可以培养学生灵活解决数学问题，从多个角度思考、探索数学问题的能力，使学生深入认知和理解数学对象。三角形的认知和学习从小学阶段就开始，初中时期学习了与三角形性质有关的勾股定理，三角形“四心”等基础性的知识内容。高中有关“解三角形”的知识点也会应用到之前学过的内容。

高一阶段讲解“利用向量综合知识解三角形”的相关知识点时，教师要通过实际问题切入课题，加深学生对向量加法概念形成及其意义的理。使学生学会利用向量法对三角形已有的性质进行证明，发现新的性质，培养学生利用高中数学知识重新“认识”、解决数学问题的学科思维。

（二）构建合作学习小组开展教学

新课程标准对高中数学教学做出了新的指示和要求，教师要根据教育改革要求对数学课程目标、教学方法做出更新和调整。以培养学生的逻辑思维和数学综合能力为教学目标。正确认识学生的主体地位，在潜移默化的教学中提升学生的逻辑思维和数学能力。为此，可以构建合作学习小组，根据学生基本学情和教材知识点，以学生课堂表现和学习积极性为标准将全班学生分为若干个学习小组，再立足数学教材内容，设计相应的问题，组织学生展开讨论。

以“用向量法研究三角形的性质”相关知识的教学为例，可以引导学生从三角形的“四心”回顾初中所学的三角形性质，如：三角形的三条中线相交于一点，这个交点叫做三角形的重心。重心分中线成 2：1 的两条线段，三角形的三条垂线相交于一点，这个交点叫做三角形的垂心，三角形的三条角平分线相交于一点，这个交点叫做三角形的内心等，并利用动图呈现三角形的性质。其中以三角形中线的性质为例，从一条中线到两条中线再到三条中线，为进一步研究三角形中线的性质做铺垫。

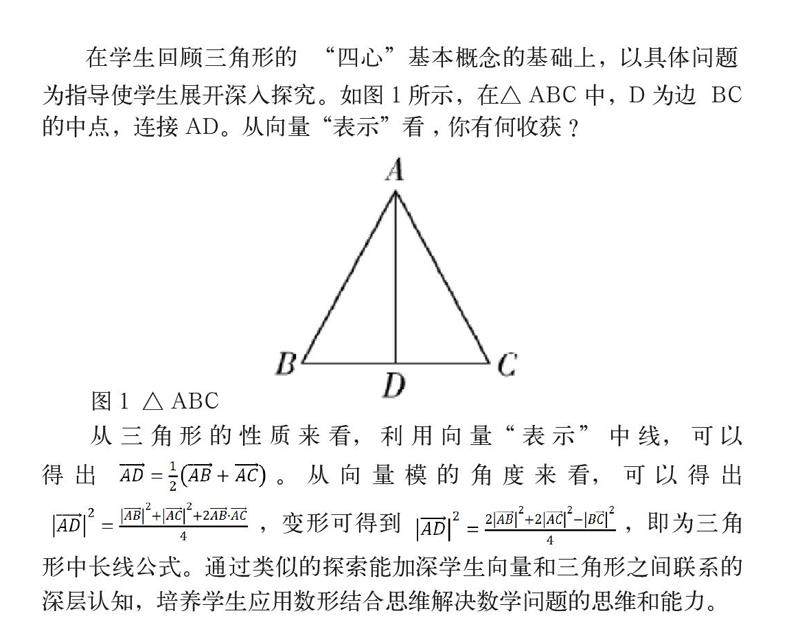
在学生回顾三角形的 “四心”基本概念的基础上，以具体问题为指导使学生展开深入探究。如图1所示，在△ABC中，D为边 BC 的中点，连接AD。从向量“表示”看，你有何收获？

从三角形的性质来看，利用向量“表示”中线，可以得出。从向量模的角度来看，可以得出，变形可得到，即为三角形中长线公式。通过类似的探索能加深学生向量和三角形之间联系的深层认知，培养学生应用数形结合思维解决数学问题的思维和能力。

（三）合理创设教学情境，激发学生兴趣

情境教学法是课程改革背景下衍生出来的一种新型教学方法，可以根据高中学生的认知规律、学习能力和思维方式创设多种教学情境，如现实情境、数学情境、科学情境、信息化教学情境等。在数学课堂上构建多元化的教学情境可以激发学生的学习兴趣和求知欲，使学生将数学知识与情境元素建立联系，加深对数学知识内容的理解和记忆。例如，在求解有关三角形的数学问题时，可以通过多媒体设备播放工业生产等现实行业中三角型形相关知识点的实用性，使学生在实际应用场景中感受和理解数学知识的实用性，改变以往教学中对数学的理解仅停留在理论和书本层面的局限性。构建具体情境可以引导学生从多个思维角度记忆和理解数学关键知识点，在循序渐进的教学中强化学生数学综合能力，激发学习潜力，感受到数学知识的魅力。

结束语：

综上所述，高中数学具有整体性、系统性，不同数学知识点之间存在千丝万缕的联系。求解三角形的方法和技巧比较多，向量法是其中之一。向量是几何知识代数知识的衔接工具，掌握向量综合法解决数学问题的技巧有助于培养和锻炼学生的数学逻辑能力、抽象能力，培养学生从多个角度思考、解决数学问题的思维。教师要根据教材内容和高中学生的多元化发展需求创新数学教学模式，为促进学生实现多元化发展营造良好的学习氛围。

参考文献

[1]吴万征.单元整体视角下的高中数学概念复习教学的实践与探索——以“解三角形”一轮概念复习教学为例[J].中学数学月刊，2022（12）：24-28+37.

[2]夏克淮.高中数学解三角形问题的策略分析[J].天天爱科学（教育前沿），2020（10）：163.

[3]李玉莲.例讲高中数学解三角形问题[J].数理天地（高中版），2022（18）：12-13.