
- 收藏
- 加入书签
基于ARIMA模型预测分析的中国新能源电动汽车发展趋势
摘要:本文通过时间序列分析,从生产消费和基础设施建设两个方面,探讨了未来10年中国新能源电动汽车的发展情况。利用ARIMA模型进行预测,选择中国新能源汽车产销量和充电站数量作为关键指标。结果表明新能源汽车销量未来十年将继续增长,对环境投资可能带来较高收益。模型预测的充电桩数量也呈现明显增加趋势,为电动汽车充电基础设施建设提供支持,为未来中国新能源电动汽车市场的发展提供了深入的理解和预测。
关键词:新能源电动汽车;ARIMA模型;发展趋势
1指标选取及时间序列分析
本文选用了中国新能源汽车产量、销量和新能源汽车充电站作为预测的项目,通过查阅文献可知,这几个指标从某种意义上能够代表新能源汽车的发展情况。
针对新能源汽车的产量和销量,它们几乎是一致的,在后续的分析预测中,只需要选用其中一个指标分析即可。自2020年后,新能源汽车的销量产生了飞速增长。不同类型的新能源汽车充电桩的变化情况是存在差异的。其中,交流一体充电桩的数量随着时间推移呈现出递减的趋势,可能是由于其性能的问题导致。
1.1突变点检测
通过时间序列分析,从生产消费情况和基础设施建设情况两个角度分析近十年的中国新能源电动汽车,并进行突变点检测,后半段的数据无法用于测试。其次考虑到搜集到的数据是按年进行统计的,不存在季节趋势,数据量较小,故采用了比较经典的ARIMA模型进行时间序列分析,对未来十年的情况分别进行预测。且选取ARIMA模型进行分析,通过差分保证时间序列的平稳,再使用AR和 MA模型预测结果。
通过突变点检测得出新能源汽车产量销量快速变化的转折点的数学依据,从而为ARIMA 模型的训练提供一定的依据,突变点检测主要采用KNN进行。考虑到那些异常点附近也可能在在异常点,即异常点和异常点之间是非常接近的,本文选取K=3,尽可能避免较为相近的情况,突变点检测的结果如下所示。
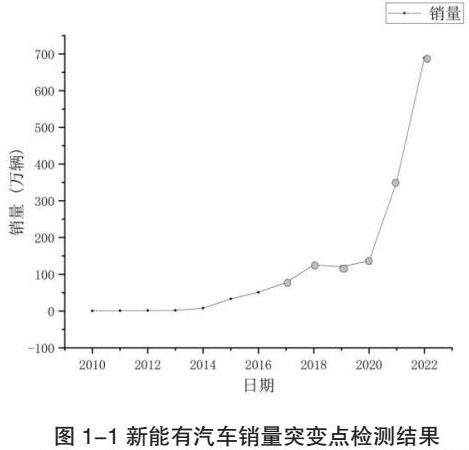
图1-1 新能有汽车销量突变点检测结果
由图1-1可知,突变点都聚集在新能源汽车的最新几年,即2017年到2022年,由于时 间序列的训练测试方法一般是采用前半部分进行训练,后半部分进行预测,而根据突变点检测,新能源汽车的销量变化主要体现在后半段,后长段的数据无法用于测试,在后续的ARIMA模型构建中,是无法进行效果评估的。
2 ARIMA模型构建
2.1算法原理
ARIMA时间序列模型是将自回归移动平均模型进行差分处理,其主要的方法是建模、评估、验证以及控制,表示为ARIMA(pd,q), 其中参数以及意义下:
AR(p)—自回归模型;MA(q)—移动平均模型;p—自回归阶数;d—数据处理过程的差分次数;q—移动平均阶数。
模型的主要思想是在已知数据是按照时间发展顺序形成的情况下,将其看成一个随 机序列,而后用数学建模的方法描述这个随机序列,这个序列一具被识别出来,便可以凭借当前时间序列值来预测未来的值。
回归AR(p)模型阐述的是在某一个时刻与前p个时刻之间相关的模型,如下所示:
其中,μ是自回归系数,ε是白噪声序列。可以称为,是p阶自回归过程。移动平 均模型MA(q),阐述的是如果将视作某个时期的随机干扰,即白噪声ε的时序线性组合,其中,θ是自回归系数。若ARIMA 模型的时间序列是平稳序列时,即不需要对数据进行差分化处理,便可以称为自回归移动平均过程,记为ARIMA(p,q) 。
在确定ARIMA中p,q时,需要同时对自相关系数(ACF)的截尾性和拖尾性,偏相关系数(PACF)的截尾性与拖尾性进行判断。截尾是指ACF与PACF在某阶后均等于0的性质,拖尾是指ACF与PACF在某阶后均不等于0的性质。
2.2结果分析
通过上述介绍,我们可以知道,ARIMA模型的主要建模是选取合适的p 、q 和 d。 通过每个簇的自相关系数图和偏自相关系数图,我们可以确定p和q值。通过ADF确定时间序列是否平稳,如果不平稳,则进行一次差分,进而得到当时间序列平稳时对应的d值。
考虑到ARIMA模型需要通过自相关函数和偏自相关函数来确定ARIMA 模型的阶数,人为对每个品类的图像观察确定阶数的成本较高。因此本文将采用网格搜索的方式,搜索区间为[-4,4],搜索AIC值最小时所对应的AR阶数和MA阶数,其偏相关和自相类函数图像如图2-1所示。
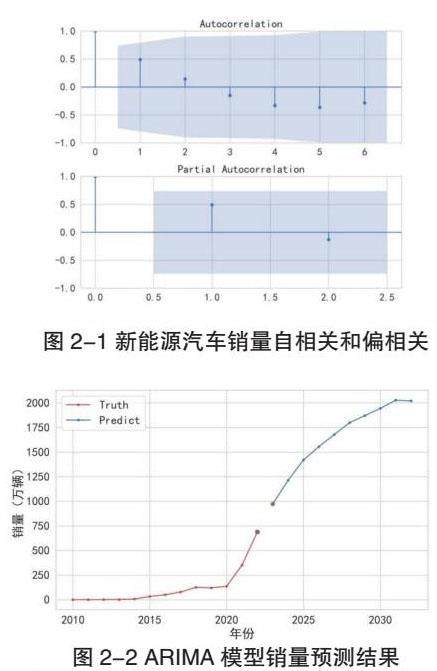
其预测走势图如下所示。可以看到,未来十年的新能源汽至发展都会呈现出蓬勃发展的状态,对新能源汽车的投资可能会有较高的收益,并且销量的增加会使得中国的环境变得更加优越。同理,按照同样的逻辑线,我们将构建好的充电桩数量预测ARIMA 模型的结果进行可视化。结果同样是明显增加的趋势,并且增加的程度是比较平稳的。
参考文献:
[1] Piccolo D. A distance measure for classifying ARIMA models[J]. Journal of time series analysis, 1990, 11(2): 153-16





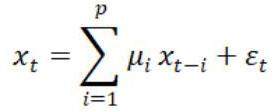

 京公网安备 11011302003690号
京公网安备 11011302003690号


