打开文本图片集

摘要：圆的认识是一节概念课，学习之前，学生对圆有一定的经验，基于经验的概念课活动设计应关注在已有经验的基础上，通过比较领悟概念本质；在技能形成的过程中，通过操作体验概念本质；在多元表征的练习中，通过思辨理解概念本质。

关键词：概念理解；活动设计；经验

【课前思考】

数学活动不仅承载着学生数学学习的过程，同时还承载着知识技能目标教学所要达成的结果。“圆的认识”一课，包含了圆的概念、画圆的技巧、圆的各部分定义及特征、圆各部分的相互关系等活动内容。从数学知识前后的逻辑关系来分析，必须要先理解圆的本质，才可以定义圆的各部分名称，然后才可以研究圆的特征。圆的定义可以是：在平面内，到一个定点的距离等于定长的点的集合。其中定点、定长和点的集合是概念的要素。对应概念的理解，定点即是圆心，定长即是半径或直径，点的集合即是动态由旋转而成的封闭曲线。

在没有教学圆的认识前，学生是否都有画圆的经验？他们又是怎样画的？在没有任何暗示的情况下，通过对五年级下学期学生进行前测，发现64%的孩子回答用圆规。在用其他方法画圆的孩子中，其中用描硬币、茶杯盖等描出圆的占大多数，说明孩子的生活经验以“描线画圆”为主。而在对用圆规画圆的学生进一步进行访谈调查，发现只有少数孩子会正确画圆，说明学生在操作上有一定的难度，需要告知和模仿练习。

“圆”是曲线围成的图形，这是生活带给学生最原始经验。在数学逻辑体系中，除了低年级对圆的直观认识，五年级旋转的动态直观也是不可忽略的前期准备。既然学生对圆已有如此充分的经验认知，概念的理解是否能从经验出发，从技能落实的过程中渗透，从任务解决的结果中提升？基于这样的设想，设计如下三个教学活动。

【教学活动】

一、多维度画圆活动，感知圆的本质

1.通过生活情境感知圆的属性

①出示生活情境

师：猎人捕获了一匹野马，用绳拴在木桩上。这匹野马用力挣扎着想要逃跑（出示野马挣扎时拉直了绳子在上下左右等方位的形态）。想象，野马挣扎的最大范围是个什么图形？（在挣扎时留下点的基础上，动态奔跑。）

生1：跑成一个圆。

生2：最大的只能是绳子拉直后旋转一圈得到的一个圆形。

师：你们是怎么想的？

生1：因为绕一个点旋转360°就是一个圆。

生2：拴马桩在那里固定了，不管野马怎么挣扎，这些最大距离的点连起来就是一个圆形。

师揭示课题：圆的认识

【教学设想：野马挣扎奔跑的情境在导入处有两层含义。一是突出点到定点等距离的运动；二是运动轨迹形成圆，圆是点到定点等距离的所有点的集合。通过演示感知，马为什么不会跑到这个圆的外面？定点。马用力挣扎，为什么还是只能跑那么大的一个圆？定长。从常见的生活情境出发，由定长留下的点到动态圆的旋转，将所有的点连接成一条封闭的曲线，唤醒学生熟悉的经验，体会圆是一条封闭的曲线，曲线上所有点到定点是等距离的概念本质。】

②圆的不同画法

师：想要得到一个圆，有很多种方法。

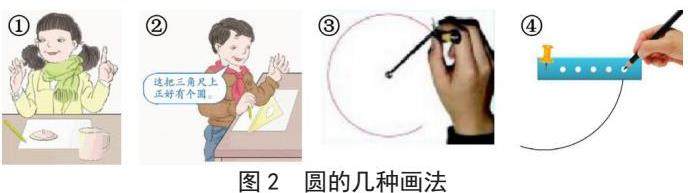
出示画圆的几种常见方法。（如图2）

想要得到一个圆，有很多种方法。

师：图上的同学是怎么画圆的呢？能画出一个圆吗？

生1：第一个图是可以沿着茶杯盖描出一个圆；

生2：第二个图是在三角板的圆形窟窿中间描出一个圆；

生3：第三个图是用钉子钉住绳子的一端定中间，绳子另一端拴住铅笔，也能画出一个圆；

生4：第四个图是用图钉钉在纸板上，铅笔穿过尺子的窟窿，也能画出一个圆。

师：在这些方法中，哪些方法跟野马奔跑得到的圆有相类似的地方呢？

生：第三个图和第四个图，中间都有像拴马桩一样的一个点，也像绳子拴马一样旋转一圈。

师：除了用这些方法能画出一个圆之外，你还有其他的画圆方法吗？请大家试一试，独立画出一个圆。

【教学设想：在生活中孩子对圆积累了丰厚的感性认识，对画圆也不陌生。在没有圆规的情况下，最简便的就是描圆形物体一周得到圆。基于学生的经验，通过比较描圆和利用定点、定长画圆的方法，体会圆概念的关键属性，在画圆的过程中凸显定点和定长的价值。】

2.通过画圆感知圆的本质。

①一画圆，尝试用自己的方法画圆。

反馈：分别说说用其他方法画圆和用圆规画圆的方法。

生1：我用硬币描出一个圆；

生2：我用两个量角器并起来描圆，但不是很圆；

生3：我的圆是用圆规画的。

师：我们很多同学与圆规都是初相识。谁能给大家介绍一下圆规的构造，以及怎样使用圆规呢？

（教师在学生介绍后，指出用圆规画圆的要领。）

②二画圆，使用圆规画圆。

师：要使所画的圆大一些，怎么办？

生1：圆规两脚尖叉开大一些画的圆就会大一些。

生2：圆规两脚叉开决定了圆的大小。

师：如果任意画圆，得到的圆就会有大有小，但如果要求全班同学用圆规画出的圆都一样大小，怎么办呢？

生：把圆规两脚之间的距离都规定一样大小。

师：好。我们一起画一个同样大小的圆。先画一条长3cm的线段，圆规的一端固定在一个端点上，一端与线段的另一个端点重合。这样就能保证圆规两脚间的距离就是线段的长。

出示画圆的视频微课。生独立画圆。

③圆的各部分名称。

师：你的定点在哪里？这个定点就是圆的圆心，通常用字母“O”表示。

师：那我们所说的定长是什么？

生：叫半径。

师：半径通常用字母“r”表示。请在你画的圆中标出圆心，画出半径，并标上字母。

师：过圆心画一条两个端点在圆上的线段叫什么？

生：直径。

师：直径通常用字母“d”表示。请大家在图上标上。

④比较各种画圆方法，感悟圆的本质特征。

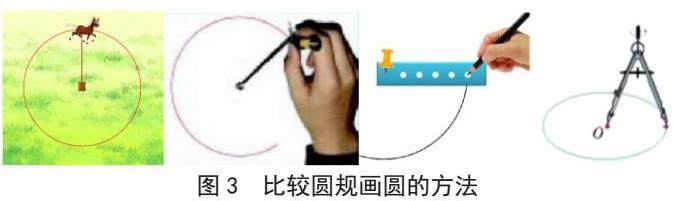
汇总以上几种画圆方法（如图3），比较：刚才的这几种画圆的方法与野马逃跑有什么相同的地方？

生：都是固定圆心，确定半径，通过旋转，画出一个圆

【教学设想：圆规画圆可以在两脚叉开的范围内画出任意大小的圆。部分学生在课外尝试过用圆规画圆，但是圆规脚尖的高低、手柄的捏法，都是影响画圆的因素，需要教师进行正确方法的示范。所以微课的示范和讲解是非常合适的。同时，在用圆规画圆的过程中，引出圆的各部分名称，与前面的活动衔接自然；同时，画圆的过程非常契合“圆是到定点的距离等于定长的所有点的集合”这一几何学的定义。】

⑤三画圆，深入理解本质。

师：请在半径3cm圆的基础上再画2个大小不同的圆。

反馈1：三个同心圆；

反馈2：三个不同位置不同大小的圆。

师：比较这两个同学画的圆，你发现了什么？

生1：圆心决定圆的位置。同一个圆心，圆就都在一起了。

生2：半径决定圆的大小。虽然圆心在一起，但半径不同，画出来的圆大小就不同。

【教学设想：理解抽象定义的本质，不是直接的告知，而是由学生自己经历建构概念的过程。三次画圆和比较，加强圆概念的各种图式和操作的关联，在不同圆位置和圆大小的比较中理解圆心和半径的特征。借助具体材料的观察比较、操作反思，理解概念的本质，是数学学习的有效方式。】

二、通过找圆心和半径等活动感受圆的特征

任务探究：在圆形纸片上，找到圆心、半径和直径。

（1）活动要求：

①找出圆心；②画出直径和半径，标出长度；③用简洁的方式记录你的发现，同伴交流并验证。

（2）反馈交流

师：你们找到圆心了吗？是怎么找到的？

生1：将圆片对折一次，两次，中间的交点就是圆心。

生2：我将圆形纸片对折一次，量一量，中点就是圆心。

生3：我没有折，量出了两段在圆上的最长线段，就是直径。中间的中点就是圆心。

师追问：大家用不同的方法都能找到圆心。对折时，这折痕是什么？这量得最长的那条线段又是谁？为什么圆心一定就在两条折痕的交点上呢？

生：因为这折痕就是直径！所有直径都经过圆心！

师：大家说的所有的直径，这样的直径你能找到多少条？

生1：无数条！

生2：因为经过一点可以画无数条直线，所以经过圆心，两端在圆上的直径也有无数条！

生3：半径也有无数条！圆上任意一点与半径连起来的线段都是半径，所以半径也有无数条。

师：通过刚才的活动，你们还发现了什么？要能补充说明理由。

生1：我们还发现圆是轴对称图形，对称轴就是直径。我们用对折验证。

生2：我们发现直径是半径的2倍，我是量出它们的长度。

生3：不量也可以证明，圆心把一条直径分成两条半径。

师：所有的直径都是半径的2倍，半径一定是直径的1/2吗？

学生齐声回答一定！

老师举起手里的大圆片，学生的小圆片。孩子们马上领悟，补充得到“同一圆内，直径是半径的2倍。”

【教学设想：自主找圆心，记录发现，并同伴交流验证。这个活动过程富有思维价值。学生通过直观经验知道在一个圆中最长的线段是直径，可以直接量直径，再在直径中找圆心。之前已经认识了圆是轴对称图形，部分学生马上会想到对折，而且知道这条折痕就是直径，接着再在这条直径中找圆心。或者将圆纸片不同方向对折两次，圆心一定在两条直径的交点上。通过对折两次找到圆心，和由经过一点可以画无数条直线联想到“直径有无数条”的学生，实际上在运用了逻辑推理的思想。】

三、生活中理解辨析圆的特征。

师：圆在生活中随处可见，你能想到哪些？

生举例。

①出示钟面，你能找到静止的圆，还能找到隐藏的会动的圆吗？

②圆形套圈游戏：为什么要设置成圆形才公平？

③汽车轮胎：为什么要是圆形的？

师：如果将生活中的圆形设置，对应今天对圆的理解，你又能对“墨子----圆，一中同长也！”作怎样的解释？

【课后反思】

这是一节基于经验的概念教学，主要体现在以下三点：

1.在已有经验的基础上，通过比较领悟概念本质

学生的经验有来自于生活的经验和知识的积累。学生积累的感性经验，不但可以进一步理解圆的特征，而且也为进一步画圆奠定了基础。从情境图的野马逃跑拉直缰绳，而后呈现圆的不同画法，比较领悟定点、定长；比较圆规画法、绳子画法、野马脱缰之间的异同，明确圆规两脚间的距离就是半径。通过比较将抽象的概念在形象的情境中反复呈现，逐步感知。

2.在技能形成的过程中，通过操作体验概念本质

借助活动，在多次用圆规画圆中既掌握圆的技巧，又进一步理解圆的本质特征。画圆可以分成利用其他工具画圆和圆规画圆两个方面。通过情境的比较理解定点和定长，理解用圆规画圆的方法。用圆规画圆看起来是一个操作的过程，但从前测中，我们发现学生常常是画不工整。本节课的三次画圆各有环节目标，第一次画圆是基于学生的原始认知，第二次经历定长画圆，理解定长即半径，即圆规两足之间距离，第三次操作是进一步体会圆心定位置，半径定大小。

3.在多元表征的练习中，通过思辨理解概念本质。

数学教学既要基于学生已有学习与生活经验，唤醒学生学习的内驱力，同时也要通过丰富的数学学习活动让学生的数学活动经验有所发展。

通过任务驱动下的折纸活动操作，学生在解决问题，探索发现，验证反思的过程中积累丰富的数学活动经验。这个开放式的活动，首先学生通过折找到圆心，理解半径、直径与圆心之间的关系。利用画图形、量数据，让学生用图式、语言的、文字符号的、动作等不同的表征方式进行讨论、思辨，从而加深理解圆的本质特征。

参考文献：

[1]数学课程标准[M]；北京师范大学出版集团；2022年.

[2]曹一鸣；新版课程标准解析与教学指导[M]；北京师范大学出版集团；2022年.

[3]郜舒竹；小学数学这样教[M]；华东师范大学出版社；2021年.