打开文本图片集

摘 要：高中数学中的立体几何，作为培养学生空间想象力和逻辑思维的重要分支，其教学质量直接关系到学生逻辑推理素养的形成。然而，当前立体几何教学中普遍存在重计算轻推理、重结果轻过程的现象，导致学生在面对几何证明和抽象推理时显得力不从心。因此，如何在立体几何教学中有效促进学生逻辑推理素养的培养，成为教师亟待解决的问题。

关键词：高中数学；几何直观教学；逻辑推理素养

一、在高中数学立体几何教学中如何促进逻辑推理素养的培养的意义

（一）立体几何的学习要求学生具备空间想象能力，这种能力的培养本身就是逻辑推理素养的一部分。学生在理解立体图形的性质和关系时，需要通过逻辑推理来构建和验证自己的空间想象。

（二）立体几何教学中的证明题是培养学生逻辑推理素养的有效途径。证明题要求学生不仅要知道结论，更要理解结论的来龙去脉，这需要学生运用逻辑推理来构建证明的逻辑链条。通过证明题的训练，学生能够学会如何从已知条件出发，逐步推导出结论，这种思维方式对于提高学生的逻辑推理能力至关重要[1]。

（三）立体几何教学中的问题解决过程，也是培养学生逻辑推理素养的重要环节。在解决实际问题时，学生需要将抽象的几何概念与具体情境相结合，通过逻辑推理来找到解决问题的方法。这种从抽象到具体，再从具体到抽象的思维转换，能够有效提升学生的逻辑推理能力。

二、在高中数学立体几何教学中如何促进逻辑推理素养的培养

（一）创设情境，引出定义

为了激发学生探究的兴趣，培养学生的爱国主义情怀，促使学生直观感知直线与平面垂直的本质，教师应结合教学内容，及时利用多媒体播放并介绍日晷这种我国古代普遍使用的计时仪器以及计时原理，然后要求学生逐一思考以下几个问题：

问题1：古代在制作日晷时，如何能够准确判断晷针与晷盘垂直。

问题2：为了有效解决上述问题，如何将日晷计时过程数学化。

问题3：试着应用自己的语言，归纳总结出直线与平面垂直的定义。

（二）设置问题，得到猜想

为了促使学生掌握逻辑推理规则，有效引发学生的认知冲突，教师应根据线面垂直的定义，推理出若要使得晷针与晷盘垂直，则需要判断出晷针与其在晷盘内形成的每一个影子垂直，显然这是非常困难的，也是不太现实的[2]。于是，为了降低学生思考的难度，教师应采用类比方式，就地取材，要求学生观察类似教室内暖气供水管与屋顶面、书立侧棱与书立底面之间的特征（如图1、图2所示）。

由此引导学生猜想出若想获得一条直线与平面垂直，则需要这条直线与该平面内的两条相交直线垂直即可。

（三）操作确认，规范证明

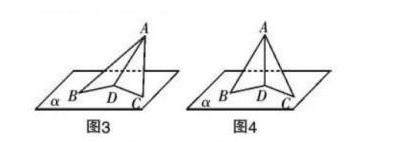
为了有效验证学生的猜想，帮助学生在课堂上获取基本活动经验，有效强调猜想中“两条”“相交”等关键词语，教师应引导学生通过如图3、图4的方式完成教材中所设计的探究活动，并思考教材所提出的问题。

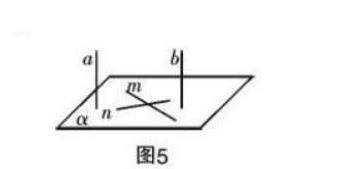
然后要求学生应用图形语言和符号语言表示直线与平面垂直的判定定理，并要求学生结合日常实际列举生活中直线与平面垂直的实例。在此基础上，为了进一步帮助学生厘清概念和定理之间的逻辑关系，有效规范相关的证明过程，教师还应及时呈现如下题目，要求学生先行分析思路并进行证明，然后由教师板书示范过程。

如图5所示，已知a∥b，若a⟂α，则试求b⟂α。

（四）变式练习，归纳反思

为了进一步加深学生对直线与平面垂直判定定理的理解，促使学生在反思归纳时有目标、有方向，教师还应及时结合教材例题和相关的练习题目，要求学生独立完成如下的变式题目：

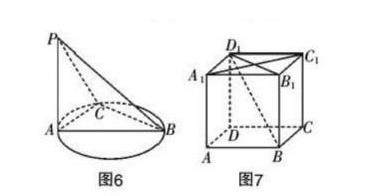
（1）如图6所示，已知PA垂直于圆O所有直线，其中C为圆周上的一点，AB为圆O的直径，①证明BC⊥平面PAC;②证明BC⊥PC;③写出图中所有的直角三角形。

（2）如图7所示，已知正方体ABCD-A1B1C1D1，证明AC⊥平面BBD。

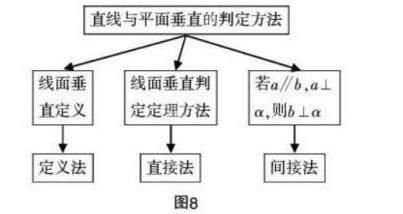
在此基础上，要求学生以“如何判定某一条直线与平面垂直”为主题进行充分讨论，并引导学生通过如图8所示的知识结构图进行总结，有效帮助学生完善自己的知识体系[3]。

（五）对学生内容进行归纳，提高学生的语言组织的能力

教师要引导学生归纳这些规律，并且指导学生如何进行运用，立体几何常用的思想方法有平移，翻折，旋转，借用、替代等等。教师要让学生对这些方法进行练习，从而更好的判断出在遇到问题时需要使用哪些方法。

例如，在判断空间直线的位置关系时，最佳的方法是构建恰当的几何图形，用构建的几何图形更直观的判断位置关系。在遇到证明点或面共线的问题时，通常是证明点在同一条直线上，来对问题进行解决。在翻折问题时，则需要各个量在折前和折后的变化与否，从而对问题进行分析和解决。教师要引导学生回顾旧知识，总结自身的学习方法，提高学生的语言组织能力和逻辑思维能力[4]。

结语：

立体几何教学在高中数学教育中对于促进逻辑推理素养的培养具有不可替代的作用，能够使数学思维得以生发和创新，提升学生的几何学习意识，促进空间几何能力的发展。通过空间想象能力的培养、证明题的训练、问题解决过程的实践以及严谨思维习惯的建立，学生还能够在立体几何的学习中不断提升自己的逻辑推理能力，为未来的学习和生活打下坚实的基础。

参考文献：

[1]徐晓华.基于逻辑推理素养下的高中数学立体几何教学策略探析——以"直线与平面垂直的判定"为例[J].数学教学通讯， 2021， 000（033）：P.43-44.

[2]王耀.浅析立体几何教学学生逻辑推理核心素养的培养[J].数理化解题研究， 2018（9）：2.

此论文为课题《在立体几何中逻辑推理素养的培养研究》阶段性成果