打开文本图片集

摘要：本文对大概念视角的含义进行简要概述，并针对大概念视角下的小学数学单元整体教学实践方法，从大概念的提取、单元目标的确定、核心问题的引领和单元课时的设计这四个方面展开探究与思考，以期能够为小数学教学工作提供可参考性的建议。

关键词：大概念视角；小学数学；单元整体教学

2022版新课标在“课程实施”部分的“教学建议”中，特别提出了“探索大单元教学”“重视单元整体教学设计”。新课标的发布带来了新的课程理念和新的改革行动，也带来新的融合问题和新的机遇挑战。基于大概念展开单元整体教学已成为当前学科教学中落实核心素养的趋势。数学大概念指向数学核心内容与核心教学任务，是一种建立在事实基础上的深层次、可迁移的概念，它能反映数学本质，是将数学关键思想和相关内容联系起来的关键“锚点”。接下来笔者结合自身的课题研究与实践谈谈如何从大概念视角来开展单元整体设计和教学工作：

一、深究教材本质，提取单元大概念

小学数学学习一般以“册”为基准，以“单元”为目标，分“课时”进行，教学中师生都较少关注知识间的关联。究竟该如何确定单元整体教学的大概念呢？这就需要教师深研课程标准、深入学生实际、深究教材本质，将此主题单元处于核心地位的数学思想和理念，及所需培养的学生的高阶思维作深刻分析与把握。

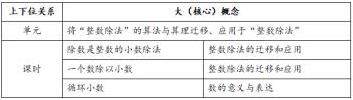
例如，人教版教材五年级上册《小数除法》单元中，“除数是整数的小数除法”是单元的起点，“一个数除以小数”其实是“除数是整数的小数除法”的变式，其他知识都围绕这两种小数除法展开并逐步深入。如果说“除数是整数的小数除法”是基于“整数除法”的迁移，那么“一个数除以小数”则是基于“除数是整数的小数除法”。归根结底还是基于“整数除法”，由此，我们可以确立单元与课时的核心概念。

“小数除法”的关键是理解小数除法的算理，能从读数单位的角度解释算理，掌握小数除法的计算方法。能够将新的知识转化成已知的知识，并将之迁移应用，解决未知的问题。

二、立足于大概念，确定单元教学目标

基于大概念视角的单元整体教学工作，要根据本单元需要解决的问题，来制定教学目标。该目标需要具备较强的统领性，能够对上位知识进行概括与总结。此外，要注重体现学科的育人价值，注重知识目标、能力目标、情感价值目标这三者之间的融合，强调学生知识的建构与转化、知识的有效迁移。

例如，人教版教材五年级上册《多边形的面积》，在单元大概念的统领下，依据核心素养要求，我们对本单元的目标进行梳理和整合，最终确定单元总目标为：初步学会运用转化的思想分析几何问题，能够根据问题的特点用不同的方法将未知图形转化成已知图形。理解并掌握多边形面积计算公式的产生过程，初步培养学生的推理意识，发展空间观念。

三、核心问题引领，助力核心素养落地

立足于学生的认知水平设置课时核心问题，营造适宜的课堂环境，让学生能独立思考分析、合作讨论判断，在思考、分析、讨论的过程中进行合理的判断，实现学生由“低阶思维”发展为“高阶思维”。核心问题凝练、探究任务聚焦，留足时间，让学生探究与思考，发展推理意识，让数学核心素养能够落地生根。

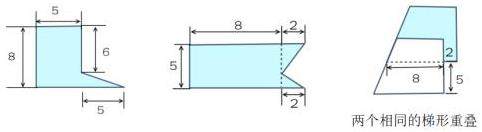
例如，在教学人教版教材五年级上册《多边形的面积》中“求组合图形面积”时，可设置问题“8×5＋5×2÷2这道算式能求出下面涂色图形的面积吗？请说说其中的道理。”驱动学生观察组合图形，结合特征，通过转化等形式解决问题。

上述核心问题引领的探究任务，简要、干净，为学生留出充足的自主推理的空间，为实现学生学习方式转变奠定基础。在对话交流时，学生差异化的方法让大家感受到数学的魅力——既可以从图形“分割”的角度进行转化，也可以从图形“整合”的方向进行思考。在双向思维中实现推理意识的发展。

四、细分课时目标，系统关联整体建构

优秀的单元设计应当是为学生提供足够的时空并促使学生以自己的方式探讨问题和观点的设计。具体而言，设计单元整体教学时，应围绕大概念注重三个方面的改变：一是重构教材，变点状分散为系统关联。二是重建教学，变逐个击破为整体建构。三是重塑过程，变课堂学习为课程研究。因此，根据不同课型在单元整体教学中的地位和功能，我们教师要上好四种课：知识种子课、方法生长课、思维拓展课、整理练习课。

1.知识种子课

种子的价值在于孕育与萌芽，因此知识种子课的关键在于本单元新知与相关单元旧知的对接，重在基础性知识的生根，重在基本性方法的培育。因此，知识种子课在教学时不宜过快过急而浅尝辄止，不宜蜻蜓点水般一带而过，而是需要老师慢慢地教，学生细细地学，要学得“通透”。

例如，人教版六年级《分数除法》单元的例题1就属于典型的知识种子课。这是本单元的第一个例题，教学的是分数除以整数的算理与算法。在教学时要做到三个“通透”：首先是新旧知识的通透，要回溯除法的源头，联系整数除法的含义理解分数除以整数的算理；其次是算理算法的通透，要回到直观操作，联系面积模型探索算法背后的算理；再次是抽象推理的通透，要充分感知并逐步抽象，从探索算理到理法相融，培养学生的运算能力和推理意识。

2.方法生长课

方法生长课的价值在于从知识到经验的累积，重在方法性策略的提高，重在关键性技能的生成。方法生长课的关键在于生长与迁移，要引领学生由此及彼、由浅入深地丰富知识内涵，理解方法本质，要发挥学生的主动性和探究性，要学得“扎实”。

例如，人教版六年级《圆柱和圆锥》单元的第三课时“圆柱的侧面积和表面积”从单元整体教学设计的视角来看，本节课属于第二种典型课——“方法生长课”。课始，我出示一个圆柱形状的茶叶罐让学生观察并思考：要制作这样的茶叶罐，会遇到哪些问题？让学生充分交流自己的想法之后紧接着追问：侧面商标纸的面积该怎么求？学生提出要把商标纸剪开看看是什么形状。大家经过讨论，一致认为不沿着一条直的线剪容易歪斜。然后指名一个学生上台，演示沿着圆柱的高（即商标纸的接缝处）剪开，学生清晰地看出侧面展开得到一个长方形，长方形的长相当于圆柱底面的周长，宽相当于圆柱的高。

3.思维拓展课

思维拓展课的价值在于对数学本质的深度理解，重在一般性方法的形成，重在思维能力的发展。思维拓展课的关键在于由具体到抽象、由数学到生活、由表面到深刻，进而帮助学生实现从方法到能力的发展，从能力到思想的延伸，因此要学得“灵活”。

例如，人教版六年级《分数除法》单元的例题4就属于典型的思维拓展课。在前三个例题分别学习了分数除以整数、整数除以分数之后，进一步学习分数除以分数的一般性方法，并由此拓展开去，进而形成“甲数除以乙数（0除外），等于甲数乘乙数的倒数”。教学时体现三个“灵活”：首先计算方法的灵活，只要是除以一个数，可以是分数，也可以是整数甚至小数，都可以转化为乘这个数的倒数；其次是算理解释的灵活，可以用面积图进行直观演示，也可以用线段图进行数形结合，还可以借助商不变规律进行推理解释；再次是实际应用的灵活，在题组对比中探索分数除以分数的规律，在解决实际问题中感悟分数除以分数的通性通法，在算理直观和算法抽象中感悟寓理于算的数学思想。

4.整理练习课

整理练习课则主要是促进认知结构的构建，重在知识之间的内在联系，重在通性通法的内在联结，重在整体性的核心素养培养。因此，整理练习课要让学生学得“丰富”。

例如，人教版六年级《分数除法》单元的“整理与练习”课，用三个模块进行教材编排，为单元整体教学提供了基本思路。首先是“回顾与整理”，通过三个问题帮助学生对本单元知识进行整理与建构：怎样计算分数除法？比的意义以及比与分数、除法的关系是怎样的？解决有关分数和比的实际问题时如何分析数量关系？然后是“练习与应用”，通过巩固性习题、应用性习题和拓展性习题帮助学生从知识发展为技能，从能力发展为素养。最后是“探索与实践”，一方面沟通分数除法与整数除法的一致性本质，另一方面通过画图对接分数与比的内在一致性，同时联系生活实际感受分数运算和比的意义的广泛应用和有趣规律，让学生体验数学美。

当然，基于大概念的单元整体教学是新课标提出的新理念，而当下配套新课标的新教材尚未启用。在这段特殊的过渡期，需要我们积极思考并行动起来，根据学生已有的知识经验、认知水平、学习要求，结合新课标理念和旧教材编排，大胆实践，“系统规划单元教学目标，整体把握结构化的课程内容，选择能促进学生思考的教学方式，在教学中整体设计，分步实施。”科学合理地开展教学工作，以此提升数学单元教学效果，确保教学质量，推动小学数学教学工作高效稳定地进行。

参考文献

[1]釜文彬，基于元素及关系视界下的单元整体教学审视与重建：以“线与角”单元教学为例[J].教育科学论坛，2021（7）：21-25.·187

[2]马云鹏，吴正宪，案例式解读（小学）[J].华东师范大学出版社，2027（7）

注：本文为福建省教育科学“十四五”规划2022年度课题FJJKZX22-306阶段性研究成果之一。