打开文本图片集

摘要：反证法是初中数学教学的常用方法，在证明“至多”“至少”、无穷性、唯一性和否定性问题时发挥重要作用。本文以鲁教版教材实例分析反证法在这四类问题证明中的应用，阐述其独特优势。教学中应引导学生把握反证法思路，注重培养逻辑推理能力，并根据问题灵活选择恰当证明方法。合理运用反证法，可提高学生数学素养。

关键词：初中数学教学；反证法；数学证明；逻辑思维

引言

反证法是重要的数学证明方法，培养学生逻辑思维的有效途径。《义务教育数学课程标准（2022版）》明确要求引导学生经历数学发现过程，感受数学思想方法。反证法作为间接证明，对培养创新意识和逻辑推理能力意义重大。本文将通过分析鲁教版教材实例，探讨在教学中渗透运用反证法，引导学生掌握这一重要思维工具，提升数学综合素养，为未来学习奠定基础。同时，教师应注意方法的适用性，针对不同问题灵活选择恰当的证明方法，避免生搬硬套。只有合理运用，才能真正发挥反证法的独特价值。

一、证明“至多”“至少”问题

反证法是初中数学教学中常用的一种解题方法，特别适用于证明“至多”“至少”类型的问题。其基本思路是：假设与题设结论相反的情况成立；根据题设条件和数学定理，推理出矛盾或荒谬的结果；由于假设导致矛盾，说明假设不成立，从而证明了原命题。反证法让一些不易直接证明的命题有了清晰的证明路径。在教学中，教师应注重引导学生理解反证法的逻辑思路，掌握运用反证法解题的关键步骤，培养学生的逻辑推理能力。同时还要认识到并非所有命题都适合用反证法证明[1]。合理运用反证法，可以简化证明过程，提高解题效率。

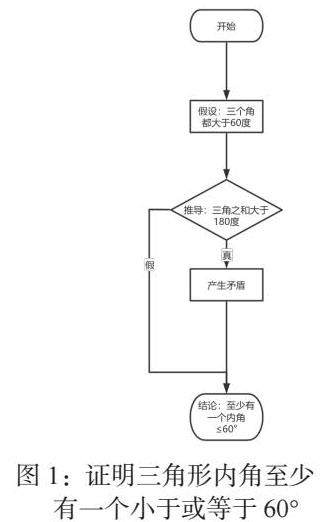
在鲁教版初中数学中，常常会遇到一些“至多”“至少”类型的问题。例如，证明“在三角形 ABC 中，至少有一个内角小于或等于 60°”。假设三个内角都大于 60°，那么∠A＞60°，∠B＞60°，∠C＞60°，则∠A+∠B+∠C＞180°，这与三角形内角和为 180°矛盾。所以假设不成立，即三角形 ABC 中至少有一个内角小于或等于 60°。反证法在这类问题中，通过先假设与结论相反的情况，然后推出矛盾，从而证明原结论的正确性。它让原本难以直接证明的“至多”“至少”问题有了清晰的解决路径。如图1：

二、证明“无限性”问题

在证明质数有无穷多个这一无限性问题时，反证法再次发挥了重要作用。通过假设质数有限，构造一个新质数，推出矛盾，间接证明了原命题。这个过程巧妙地绕开了直接证明无穷多个质数的困难，为解决无限性问题提供了新思路。在教学中，应引导学生理解这一过程中的逻辑推理和创造性思维，培养数学直觉。同时，还要强调这种证明方法的特殊性，避免学生想当然地用反证法证明所有无限性问题[2]。教师应针对不同问题，灵活选择合适的证明方法。

鲁教版中有一些关于无限性的问题。比如证明“质数有无穷多个”。假设质数只有有限个，设为 p1，p2，p3，pn。令 N = p1p2p3…pn+1。若 N 为质数，则与质数只有有限个矛盾；若 N 为合数，那么 N 必然能被某个质数整除，而这个质数不在 p1，p2，p3，pn 中，这也与假设矛盾。所以质数有无穷多个。在处理无限性问题时，反证法通过假设有限的情况，然后推出矛盾，巧妙地解决了直接证明的困难，为我们打开了证明的新思路。

三、证明“唯一性”问题

在证明“在一个三角形中，过一个顶点作一条直线将三角形分成两个面积相等的三角形，这样的直线是唯一的”这一唯一性问题时，反证法再次发挥作用。通过假设存在两条这样的直线，根据三角形面积公式，推出两直线重合的矛盾，从而证明了原命题。这一过程体现了反证法“假设不唯一，推出矛盾，确定唯一性”的思路。教学中，应引导学生理解这种思路，培养逻辑推理能力。同时，要注意唯一性问题的证明方法多样，应根据具体情况灵活选择，避免过度依赖反证法[3]。

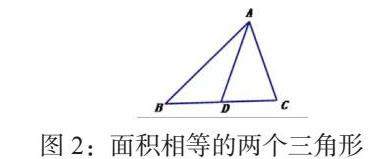
在鲁教版数学中，对于唯一性的证明也可借助反证法。例如证明“在一个三角形中，过一个顶点作一条直线将三角形分成两个面积相等的三角形，这样的直线是唯一的”。假设存在两条这样的直线 AD 和 AE。由于直线 AD 和 AE 都将三角形分成两个面积相等的三角形，那么根据三角形面积公式，可得 BD×高=BE×高（设高相同），即 BD = BE，这意味着 D、E 两点重合，所以这样的直线是唯一的。反证法在唯一性问题的证明中，通过假设不唯一，然后推出矛盾，从而确定其唯一性。如图2：

四、证明“否定性”问题

反证法是一种重要的数学证明方法，在初中数学教学中有广泛应用。它通过假设一个命题的否定形式，然后推导出矛盾或荒谬的结论，从而间接证明原命题成立。这种方法特别适用于证明存在性、唯一性以及一些难以直接证明的命题。反证法体现了数学逻辑的严谨性和创造性思维，能培养学生的逻辑推理能力。在教学中，教师应引导学生理解反证法的基本思路，掌握运用该方法解题的关键步骤，同时注意反证法的适用范围，灵活选择恰当的证明方法。

鲁教版中也有一些否定性的命题需要证明。比如证明“一个三角形不能有两个直角”。假设一个三角形有两个直角，不妨设∠A = ∠B = 90°，那么∠A+∠B+∠C = 90°+90°+∠C＞180°，这与三角形内角和为 180°矛盾。所以一个三角形不能有两个直角。对于否定性问题，直接证明往往比较困难，而反证法通过假设结论不成立，然后推出矛盾，有力地证明了原命题的正确性。

结语

综上所述，反证法是初中数学的重要证明方法，在证明至多至少、无限性、唯一性和否定性问题时具有独特优势。教学中，教师应加强引导，帮助学生理解反证法的思维过程，培养学生的逻辑思辨能力。同时，要注意方法的适用性，针对不同问题灵活选用证明方法。这样，学生不仅能掌握反证法这一思想方法，更能提升数学素养，为未来学习打下坚实基础。

参考文献

[1]陈悦，赵临龙.数学“反证法”理论的分析及其在中学数学中的应用[J].科技风，2024，（07）：118-120.

[2]冉秀玲.初中数学中反证法的教学现状及改进途径[D].西南大学，2022.

[3]吴连成.核心素养观下“反证法”的初中数学教学现状研究[D].温州大学，2020.