摘　要：逻辑推理能力是数学学科核心素养的关键维度，但传统教学往往割裂了知识学习与思维发展的有机联系。" 问题解决" 模式以问题为驱动，引导学生在分析、猜想、验证的过程中自然建构推理能力。这种教学转型不仅关注解题结果，更重视思维过程的规范化与策略化，为数学深度学习提供了新路径。基于此，以下对基于“问题解决”模式的高中数学逻辑推理能力培养策略进行了探讨，以供参考。

关键词：“问题解决”模式；高中数学；逻辑推理；能力培养

引言

当前高中数学教学对逻辑推理能力的培养多停留在题型训练层面，未能有效建立思维方法与问题解决的联系。" 问题解决 " 模式通过创设真实问题情境，将逻辑推理过程显性化，有助于学生掌握数学思维的底层规律。这种培养方式强调从具体问题抽象出推理框架，对提升学生数学核心素养具有实践价值。

一、“问题解决”模式的内涵

" 问题解决 " 模式是一种以真实问题为驱动、以思维发展为导向的教学范式，其核心在于通过系统化的问题处理过程培养学生的数学逻辑推理能力。该模式强调将数学知识置于具有挑战性的问题情境中，引导学生经历 " 问题识别—策略选择—方案实施—反思优化 " 的完整认知过程。在问题识别阶段，注重培养学生从复杂情境中抽象出数学本质的能力；策略选择环节着重训练学生基于已有知识构建解决方案的推理能力；方案实施过程强调逻辑表达的严谨性与解题步骤的合理性；反思优化阶段则促进学生批判性思维的养成。与传统解题训练不同，" 问题解决 " 模式更关注思维过程的可视化与规范化，要求学生在问题处理中明确呈现假设、推理、验证等思维要素，从而将隐性的逻辑推理过程转化为显性的思维操作。这种教学模式通过创设阶梯式问题序列，使学生在解决由浅入深的问题过程中，逐步掌握归纳推理、演绎推理、类比推理等多元思维方法，最终形成结构化、可迁移的逻辑推理能力体系。本质上，" 问题解决 " 模式实现了从知识传授向思维培养的教学转型，为发展学生的数学核心素养提供了有效路径。

二、基于“问题解决”模式的高中数学逻辑推理能力培养策略

（一）创设情境, 提出问题

在数学史上，著名的" 棋盘麦粒问题" 生动诠释了指数增长的惊人力量。相传古印度宰相西萨·班·达依尔向国王提出一个看似简单的请求：在国际象棋棋盘的第一格放 1 粒麦子，第二格 2 粒，第三格4 粒，以此类推，每一格都是前一格的两倍。这个请求背后隐藏着深刻的数学原理——等比数列的奥秘。通过分析可以发现，第 Π_n 格的麦粒数遵循通项公式 a_n=2^n-1 。运用错位相减法推导，前 n 项和 S_n=2ⁿ-1 ，这意味着 64 格棋盘需要的麦粒总数高达 2⁶⁴–1 粒，约等于全球 2000年的小麦产量。这个经典案例不仅揭示了等比数列的爆炸性增长特性，更展现了数学抽象思维的重要性。教师可以此为基础，引导学生探究更一般的等比数列求和问题，当公比为 q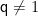（ ）时，前 n 项和公式为 S_n=a₁(1-qⁿ)/(1-q) ，其中蕴含着丰富的数学思想方法，对培养学生的逻辑推理能力和数学建模意识具有重要价值。

（二）设计问题链引导逻辑推理思维

构建层次分明的问题链是培养逻辑推理能力的有效途径。问题链设计应当遵循 " 最近发展区 " 理论，从基础性问题逐步过渡到综合性问题。在函数概念教学中，可以设计从具体函数图像观察到抽象函数性质归纳的递进式问题序列。每个问题节点都应当承上启下，前一个问题的结论构成后一个问题的思考基础。在问题链中设置关键节点问题，引导学生突破思维瓶颈，实现认知跃迁。采用 " 变式训练 " 策略，通过改变问题条件或提问角度，培养学生多维度思考能力。在立体几何教学中，可通过 " 一题多变 " 的方式，从不同视角探究几何体的性质关系。问题链的终端应当设置反思性问题，促使学生总结问题解决过程中运用的推理方法和思维策略。

（三）组织小组合作解决问题提升推理协作

小组合作学习为数学逻辑推理能力的培养提供了多维互动平台。在分组策略上，教师应综合考虑学生的认知风格、思维特点和表达能力，构建优势互补的学习共同体。每个小组可设置思维导引者、过程记录员、逻辑检验员等不同角色，通过角色分工促使学生从不同角度参与推理过程。在问题设计方面，应选取具有探究空间的开放性数学问题，如几何证明题中的多解情况或代数问题中的参数讨论，为小组协作提供充分的思维碰撞机会。实施过程中采用 " 三步质疑法 "：小组成员依次提出解题思路，其他成员进行逻辑合理性质疑，最后共同优化解决方案。教师巡回指导时，重点观察学生的推理链条是否严密，及时通过提问引导发现逻辑漏洞。在三角函数问题解决中，可让小组成员分别从单位圆、函数图像和代数变形等不同途径进行推导，再比较各种方法的逻辑关联。建立 " 思维可视化 " 分享机制，要求小组用流程图或树状图展示推理过程，培养系统性思维能力。通过定期组织跨组辩论活动，让学生在不同观点的交锋中锤炼逻辑严谨性，最终实现从个体推理到集体智慧的升华。这种协作模式不仅提升了学生的逻辑表达能力，更培养了批判性思维和团队协作解决问题的能力。

（四）加强对学生进行规律思维训练

在高中数学教育中，培养学生的规律性思维是提升数学素养的核心环节。数学作为一门系统性极强的学科，其知识体系内部存在着严密的逻辑关联，各类数学问题往往遵循着特定的解题范式。教师应当通过系统化的教学设计，帮助学生从纷繁复杂的数学现象中提炼出普适性的解题规律。具体而言，在教学实践中，教师需要精心设计具有代表性的例题序列，引导学生通过对比分析、归纳演绎等方法，逐步建立数学认知结构。比如在多元多次方程教学过程中，可采用阶梯式教学策略：先夯实一元二次方程的基础解法，再过渡到二元一次方程组的消元技巧，最终延伸到多元高次方程的系统解法。这种循序渐进的训练方式不仅能强化学生的迁移应用能力，更能培养其数学思维的严谨性和创造性。

结束语

基于" 问题解决" 模式的逻辑推理能力培养，实现了知识掌握与思维发展的统一。未来应进一步优化问题情境设计，通过阶梯式任务序列促进学生推理能力的系统提升，最终形成可迁移的高阶数学思维能力，为终身学习奠定基础。

参考文献

[1] 成娅 . 高中生计算思维、逻辑推理素养的现状及其关系研究[D]. 西南大学 ,2024.

[2] 王月 . 高中数学计数原理中的逻辑推理及教学策略研究 [D].哈尔滨师范大学,2024.

[3] 徐瑷 . 指向逻辑推理能力培养的数学问题链教学研究 [D]. 陕西理工大学 ,2024.