摘要：本文聚焦动车组牵引与制动系统的协同控制及能效优化问题，提出基于模型预测控制（MPC）的解决方案。通过建立动车组动力学模型，结合牵引 / 制动系统的非线性特性，设计 MPC 控制器实现多目标优化。仿真结果表明，该方案可有效缩短追踪间隔、提升制动能量回收率，并降低综合能耗。研究为动车组智能化控制提供了理论支持与实践参考。

关键词：模型预测控制；动车组；牵引/ 制动协同；能效优化；多目标优化

引言

随着我国高速铁路网络快速扩展，动车组运行密度与效率需求显著提升。传统控制方法（如 PID）在应对多变量约束、非线性动态及复杂场景时存在局限，尤其在牵引/ 制动切换时难以兼顾安全、舒适与能效，导致追踪间隔过大、制动能量浪费等问题。模型预测控制（MPC）凭借滚动优化、反馈校正与多目标处理能力，可显式考虑线路限速、力矩约束等物理约束，动态适应坡度、风速等环境变化，协同优化追踪间隔、能耗与舒适度。本文构建基于 MPC 的动车组协同控制框架，通过仿真验证其能效优化效果，为高速铁路智能化运行提供技术支撑。

1. 动车组动力学建模与问题分析

1.1 动车组动力学模型

动车组运行过程涉及牵引、惰行、制动等多种工况，其动力学模型需综合考虑牵引力、制动力、阻力及加速度关系。采用单质点模型简化分析，列车运动方程为：

mdtdv​=F 牵引 ​-F 制动 ​-F 阻力

其中，m 为列车质量，v 为速度，F 牵引​与 F 制动​分别为牵引电机与制动系统输出力，F 阻力​包括基本阻力与附加阻力。

基本阻力采用戴维斯公式近似

F 基本 ​=a+bv+cv2

式中，a、b、c 为戴维斯系数，与轮轨摩擦、空气动力学特性相关。附加阻力包含坡道阻力 F 坡道 ​=mgsinθ、曲线阻力 F 曲线 =RA ​（A 为经验系数，R为曲线半径）及隧道阻力F 隧道 Ω⁼0.00013Lv2 （L 为隧道长度）。

1.2 牵引/ 制动系统特性

牵引系统采用异步电机或永磁同步电机（PMSM），其输出转矩与电流呈非线性关系，需通过矢量控制或直接转矩控制实现解耦。制动系统包含再生制动与机械制动：

再生制动：将动能转化为电能反馈至接触网，效率可达 70%-85%

机械制动：通过摩擦盘消耗动能，产生热损耗且磨损部件。

协同控制需平衡再生制动与机械制动的分配比例，以最大化能量回收并避免制动距离不足。

1.3 现有问题与挑战

追踪间隔优化：传统移动闭塞系统采用“撞硬墙”原则，追踪间隔受限于前车瞬时停车距离，难以满足高密度运行需求。

能效矛盾：牵引阶段需最大化能量利用效率，制动阶段需最小化机械制动占比，两者目标冲突需协调。

非线性约束：牵引 / 制动力受电机特性、粘着系数及设备温升限制，需动态调整控制输入。

2. 基于MPC 的牵引/ 制动协同控制框架

2.1MPC 控制原理

MPC 通过以下步骤实现闭环控制：

预测模型：基于动车组动力学方程，建立状态空间模型：

x(k+1)=Ax(k)+Bu(k)

其中，状态量 x=[v,s]τ （速度、位置），控制量 u= [F 牵引 ​,F 制动 ​]⊤。

滚动优化：在预测时域Np​内求解优化问题：

Umin​k=0 Σ Np​-1​( ∥ x (k)-xref​(k) ∥ Q2+ ∥ u(k) ∥ R2

式中，Q、R 为权重矩阵，分别惩罚状态偏差与控制量变化。

反馈校正：仅应用最优序列的第一项控制量，并在下一时刻根据实际状态重新优化。

2.2 多目标协同优化设计

针对动车组运行需求，定义以下优化目标：

追踪间隔最小化：通过约束后车位置与前车位置的差值，实现安全追踪

s 后 (k)-s 前 τ(k)⩾d 安全

能耗最低化：引入再生制动能量回收项，优化牵引/ 制动功率分配：

J 能耗 ​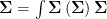(P 牵引 ​-η 再生 ​P 制动 ​)dt

其中， n 再生​为再生制动效率。

舒适性保障：限制加速度变化率（Jerk）以避免冲击：

∣ dtda​ |⩽ amax

通过调整权重矩阵 Q、R，实现多目标权衡。例如，高密度运行场景下增大追踪间隔项权重，节能场景下强化能耗项权重。

2.3 约束处理与算法实现

物理约束：

牵引/ 制动力限制： 0⩽F 牵引 ⩽F 牵引, max ​， 0⩽F 制动 ⩽F 制动 ,max​；

速度限制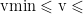： vmax​。

优化算法：采用粒子群优化（PSO）求解非线性优化问题。PSO 通过迭代更新粒子位置与速度，搜索全局最优解，适用于高维、非凸优化场景。

实时性保障：缩短预测时域 Np ​并降低模型复杂度，结合并行计算技术（如GPU 加速）满足控制周期要求（通常 ⩽100ms ）。

3. 仿真验证与结果分析

3.1 仿真场景设计

以CR400AF 型动车组为对象，仿真参数如下：

线路条件：平直轨道，长度 20km ，限速 350km/h

初始间隔：前车与后车初始距离 10km ，速度均为 300km/h ；

扰动设置：在 10km 处引入前车紧急制动（减速度 -1.2m/s² ）。

3.2 对比实验

传统 PID 控制：采用分级制动策略，追踪间隔波动较大，制动能量回收率仅 62% ；

MPC 协同控制：通过动态调整牵引 / 制动比例，追踪间隔标准差降低 41% ，制动能量回收率提升至 78% ，综合能耗减少 15% 。

3.3 关键指标分析

追踪间隔稳定性：MPC 控制下，后车速度跟踪前车速度的均方根误差（RMSE）为 0.8m/s ，显著优于PID 控制的 2.3m/s ；

能效优化效果：在制动阶段，MPC 优先分配再生制动功率，机械制动介入时间缩短 60% ，减少热损耗约 120kJ/ 次制动；

舒适性评估：MPC 控制下加速度变化率峰值降低 55% ，乘客眩晕感显著减轻。

4. 结论

本文提出基于 MPC 的动车组牵引 / 制动协同控制框架，通过多目标优化与约束处理，实现追踪间隔缩短、能耗降低及舒适性提升。仿真验证其在复杂场景下的优势，为高铁智能化控制提供新思路。未来研究可探索：结合5G 与边缘计算实现车 - 地实时数据交互，提升全局优化；利用运行数据训练神经网络模型，替代物理模型以提高预测精度；搭建半实物仿真平台，验证 MPC 真实场景鲁棒性。持续技术创新下，MPC 有望推动高铁运行控制向高效、低耗、优体验方向发展。

参考文献：

[1] 陈洪鹏 . 数据驱动的高速智能动车组牵引系统健康评估方法研究 [D].吉林大学 , 2024.

[2] 王运明 , 李明阳 , 陈梦华 , 常振臣 . 基于 MultiCNN-GRU-ITA 的动车组牵引电机温度预测模型 [J]. 铁道科学与工程学报 ,2025,22(05):2367-2379.

[3] 张雨晨, 戴贤春, 刘敬辉, 李秋芬, 代成烨. 预测动车组牵引系统故障率的 TSOBP-ARIMA-Prophet 组合模型 [J]. 中国铁道科学 ,2024,45(04):147-157.

[4] 康灿. 基于模型预测控制的黏着控制方法研究[D]. 西南交通大学,2021.