摘要：本文立足核心素养导向的初中数学教学改革需求，聚焦苏教版“方程与不等式”这一贯穿初中代数体系的核心单元，探索基于真实情境的大单元教学案例开发路径与效果评估方法。旨在为初中数学大单元教学提供可操作的实践范式，助力核心素养在课堂教学中落地生根。

关键词：真实情境；初中数学；大单元教学；方程与不等式；效果评估

引言

《义务教育数学课程标准（2022 年版）》要求通过主题整合优化数学课程内容结构，将学科知识融入真实情境学习活动中，建立横纵向相结合、层次分明的课程体系，从而增强课程内容结构的整体性，实现数学教育从学科知识本位向核心素养本位转变。初中阶段学生正处于具象思维向抽象思维过渡的关键期，真实情境能有效降低认知门槛，激发学习主动性。本文以“方程与不等式”单元为例，探讨教学案例的开发路径与效果评估方法，为破解传统教学困境提供实践参考。

一、基于真实情境的“方程与不等式”大单元教学案例开发路径

（一）锚定生活场景，创设核心驱动情境

真实情境的创设需贴合学生生活经验与单元知识本质，形成贯穿教学始终的核心线索。“方程与不等式”单元可围绕“校园周边生活服务优化”这一真实主题构建情境，将单元内容融入“文具店定价策略”“社团活动经费预算”“上学路线时间规划”等具体场景。例如以“学校筹备文化节，需采购奖品与道具”为总情境，引出“如何根据预算列方程计算可采购数量”“如何用不等式确定经费使用范围”等核心问题。这种情境设计既符合学生对校园生活的熟悉度，又能自然串联方程与不等式的知识应用场景，让学生感受到数学与生活的紧密关联，激发探究欲望。同时，情境须具备开放性与层次性，为不同学习水平的学生提供探究空间。

（二）搭建任务支架，串联单元知识体系

大单元教学案例需通过结构化任务群实现知识的系统整合，避免知识点碎片化。以“方程与不等式”单元为例，可围绕核心情境设置“基础建模—综合应用—拓展创新”三级任务支架：基础任务聚焦“用一元一次方程解决采购单价问题”，巩固方程构建与求解技能；综合任务设计“用二元一次方程组规划两种奖品搭配方案”，培养多变量分析能力；拓展任务提出“结合经费限制用不等式优化方案，兼顾成本与实用性”，实现方程与不等式的融合应用。任务之间层层递进，每个任务均嵌入真实情境细节，如“考虑商家折扣活动”“预留应急经费”等，让学生在完成任务的过程中自主构建单元知识网络，体会知识的逻辑关联与应用价值。

（三）渗透建模思想，落实核心素养目标

案例开发需将建模思想贯穿教学全过程，引导学生经历“实际问题—数学模型—求解验证”的完整过程。在“方程与不等式”单元案例中，每个任务环节都应明确建模步骤引导：面对“经费预算”问题时，先引导学生梳理已知条件与未知量，如“总经费 800 元，奖品分为单价 20 元的 A 类与 15 元的 B 类，需采购至少35 份”；再指导将数量关系转化为数学表达式，即 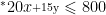，x+y⩾35^′ ”；最后通过求解、验证形成可行方案，并反思模型的合理性。同时，结合情境渗透“优化思想”“符号意识”等素养目标，让学生不仅学会“用数学”，更理解“数学如何用”，实现知识与能力的同步提升。

二、“方程与不等式”大单元教学案例的效果评估维度

（一）聚焦知识应用，评估情境解决能力

知识应用能力的评估需脱离传统纸笔测试的局限，以真实情境任务的完成质量为核心指标。可设计“校园活动方案设计”实操任务，要求学生结合给定情境独立完成“需求分析—模型构建—方案求解—效果说明”全过程，评估要点包括“是否能准确提炼数量关系”“方程与不等式模型构建是否合理”“求解过程是否规范”“方案是否符合实际需求”等。例如在“经费优化”任务中，重点评估学生能否同时运用方程计算与不等式限制，形成兼顾可行性与经济性的方案，以此判断学生对单元知识融合应用的掌握程度，避免仅关注解题正确率的片面评价。

（二）关注思维发展，评估建模与推理能力

思维发展的评估需聚焦学生在情境探究中的思维过程，而非单一结果。可通过“任务过程记录”“小组讨论发言”“建模思路阐述”等多元素材进行分析，重点关注学生是否能清晰梳理问题中的数量关系，是否能合理选择数学工具（方程或不等式），是否能对结果的实际意义进行解释与反思。例如在“路线规划”任务中，观察学生是否能从“距离、速度、时间”的复杂关系中提炼关键变量，是否能根据“赶校车时间限制”灵活调整模型，评估其逻辑推理与模型构建能力。这种评估方式能更全面地反映学生的思维品质，契合核心素养培育目标。

（三）立足学习过程，评估情感态度变化

学习态度的评估需关注学生在真实情境探究中的主动性与参与度，通过课堂观察、学习日志、小组互评等方式收集信息。重点评估学生是否主动参与情境分析与任务讨论，是否能在遇到困难时积极寻求解决方法，是否能体会到数学的实用价值并形成积极的学习情感。例如在“方案展示”环节，观察学生是否能自信表达建模思路，是否能对他人方案提出合理建议；通过学习日志了解学生对“数学有用”的认知变化。这种评估既关注学习结果，更重视过程中的情感体验，能全面反映教学案例对学生学习兴趣的激发效果。

三、总结

基于真实情境的大单元教学为“方程与不等式”单元教学提供了全新视角，其核心在于通过生活场景锚定学习目标，以结构化任务串联知识体系，用建模思想落实素养培育。案例开发需坚持“情境真实化、任务层次化、素养具体化”原则，将抽象的代数知识转化为可探究的生活问题；效果评估则需突破传统评价的局限，从知识应用、思维发展、学习态度三个维度构建多元框架，全面反映教学实效。

参考文献：

[1]孙丽.基于情境创设的初中数学项目式学习教学实践[J].数理天地（初中版 ），2025，（18）：67-69.

[2] 庞文静 . 基于真实情境的数学建模教学对初中生创造性思维的影响研究 [J]. 数理天地 （ 初中版 ），2025，（09）：163-165.

[3] 王定巳 . 情境教学法在初中数学课堂中的应用与实践研究 [A] 广东教育学会 2025 年度学术讨论会论文集（二）[C]. 广东教育学会 ， 广东教育学会 ，2025：3.

[4] 李凯 . 初中数学真实情境创设：教材样态与教学反思 [J]. 中学数学月刊 ，2025，（02）：11-14.