摘要：随着信息技术与教育的深度融合，运用动态几何软件优化高中数学教学，尤其是抽象的解析几何教学，已成为重要研究方向。本文基于《基于 GeoGebra的解析几何探究式学习校本课程的开发研究》课题成果，构建并实践了一种以 GeoGebra 为支撑的高中解析几何探究式学案编写模式。该模式以“问题引导—软件操作—观察猜想—推理验证—总结提升”为核心流程，旨在推动教学从“讲授 - 记忆”向“探究 - 建构”转型，从而有效激发学生兴趣，培养其直观想象、逻辑推理、数学抽象与数学建模等核心素养。文中详细阐述了模式的五个环节及其内在逻辑，并论证了其教学有效性与应用价值。

关键词：?GeoGebra ；解析几何；探究式学习；学案编写；数学核心素养

 

引言：

高中解析几何是沟通代数与几何的桥梁，其思想方法在整个数学体系中占有举足轻重的地位。然而，传统教学中往往过于侧重繁琐的计算与公式推导，学生难以理解图形与方程之间的动态、内在联系，导致学习过程枯燥，思维僵化。GeoGebra 作为一款集几何、代数、统计与微积分于一体的动态数学软件，其直观性、交互性和动态性为突破这一教学瓶颈提供了理想的技术工具。然而，仅仅将 GeoGebra 作为演示工具是远远不够的。要实现深度教学，必须设计一套能够引导学生主动探究、亲身体验知识生成过程的学习方案。为此，我们在课程开发实践中，系统性地总结并提炼出了“问题引导—软件操作—观察猜想—推理验证—总结提升”的探究式学案编写流程。本论文旨在对这一研究成果进行系统性总结。

一、探究式学案编写流程的核心环节解析

该流程是一个环环相扣、层层递进的有机整体，五个环节分别承担着不同的教学功能，共同促进学生知识的主动建构与能力的全面发展。

（一）问题引导——点燃思维的火种

问题是探究的起点，是驱动整个学习活动的引擎。在这一环节，学案的设计关键在于创设真实、有意义且具有挑战性的问题情境。

设计原则：问题应源于教材但高于教材，能够引发认知冲突，激发学生的好奇心和求知欲。例如，在学习“椭圆定义”时，不直接给出定义，而是提出：“到两定点的距离之和为定值的点的轨迹是什么？你能利用手头的‘绳子’（在GeoGebra 中模拟）画出这个图形吗？”

功能价值：“问题引导”将学习目标转化为学生的内在需求，为后续的软件操作和观察猜想指明了方向，避免了学生操作的盲目性。

（二）软件操作——构建动态的直观

此环节是模式的技术核心。学生根据学案指引，亲手在 GeoGebra 中进行操作，将抽象的问题转化为可视化的动态图形。

设计原则：学案应提供清晰、简洁的操作步骤，但不过度限制学生的探索空间。例如，引导学生绘制两个点 F₁ 、 F₂ ，设定定长线段 ^AB (|AB|>|F₁F₂|) ， 在 线 段 AB 上 构 造 动 点 P ， 利 用“ 轨 迹 ” 功 能， 让 点 P 在 满 足|PF₁|+|PF₂|=|AB| ( 定值) 的条件下运动，动态生成椭圆。

功能价值：通过动手操作，学生亲身经历了从“数”到“形”的转化过程，将静态的数学概念转化为可操纵、可变化的动态对象，为“观察猜想”积累了丰富的感性材料。

（三）观察猜想——孕育发现的灵感

在动态变化的图形面前，学案引导学生进行有目的的观察，并鼓励他们大胆提出猜想。

设计原则：学案应设计一系列递进式的观察任务和启发性提问。例如：“拖动点 F₁ 、 F₂ ，改变焦距，椭圆的形状如何变化？”“当焦距为零时，轨迹变成了什么？”“改变定值的大小，椭圆又有什么反应？”引导学生猜想椭圆离心率、长轴、短轴等几何要素之间的关系。

功能价值：这一环节是培养学生“直观想象”素养的关键。它训练学生从复杂现象中捕捉关键信息，提出合理的数学假设，是数学发现的重要前奏。

（四）推理验证——实现思维的升华

猜想需要通过严谨的数学逻辑加以验证。此环节引导学生从动态的“形”回归到严谨的“数”，完成从感性认识到理性认识的飞跃。

设计原则：学案在此环节应引导学生暂停软件操作，拿起纸笔，基于之前观察到的现象，进行代数推导和证明。例如，根据椭圆的定义(x − c)2 + y2 + (x + c)2 + y2 = 2a ，通过代数变换推导出其标准方程 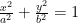，并验证之前猜想的a, b, c 关系（ c²Γ=a²Γ-b² ）是否成立。

功能价值：这是培养“逻辑推理”和“数学运算”素养的核心环节。它让学生明白，GeoGebra 的演示是探索的工具，但数学结论的最终确立必须依赖于严格的逻辑证明，从而建立起对数学严谨性的敬畏。

（五）总结提升——构建系统的认知

探究活动的最后，需要将零散的发现和结论进行系统化、结构化，并提炼出蕴含其中的数学思想方法。

设计原则：学案应通过框架图、表格或开放式问题，引导学生自主总结本节课的知识要点（如椭圆定义、标准方程、几何性质）、探究过程中所使用的方法（如坐标法、数形结合）以及核心数学思想（如转化与化归、从特殊到一般）。

功能价值：该环节实现了知识的系统化存储和方法的迁移应用，使学生不仅“学会了”，更“会学了”，有效提升了其“数学抽象”和综合归纳的能力。

二、模式的应用价值与反思

（一）显著的教学成效

激发学习兴趣：动态、可视化的探究过程，使数学变得生动有趣，极大地调动了学生的学习积极性。

深化概念理解：学生亲身经历了概念的形成过程，对解析几何“以数解形，以形助数”的本质有了更深层次的理解。

发展核心素养：该模式完整地涵盖了从直观感知到逻辑论证的数学思维全过程，有效促进了学生数学核心素养的协同发展。

（二）对教师角色的新要求

该模式的实施要求教师从知识的传授者转变为学习的设计者、引导者和合作者。教师需要投入更多精力进行课程资源的开发，特别是精心设计每一个环节的学案，并在课堂中敏锐地捕捉学生的生成性问题，进行适时点拨。

（三）实践中的注意事项

技术培训需先行：需对学生进行基本的GeoGebra 操作培训，确保技术不会成为探究的障碍。

时间管理要科学：探究式教学耗时较长，需合理规划教学进度，平衡探究深度与教学任务之间的关系。

“数”与“形”不可偏废：必须强调“推理验证”环节的不可替代性，防止学生陷入“只看不证”的浅层学习。

结论：实践证明，以GeoGebra 为平台，以“问题引导—软件操作—观察猜想—推理验证—总结提升”为流程的探究式学案编写模式，是高中解析几何教学改革的一条有效路径。它成功地将信息技术无缝嵌入到数学探究的深层认知活动中，为学生营造了一个能够亲身实践、主动思考和协作建构的学习环境。这一模式不仅提升了课堂教学的有效性，更重要的，它培养了一种科学的、理性的思维方式，为学生未来的终身学习和发展奠定了坚实的基础。未来，我们将继续深化这一模式的研究，并将其推广至更广泛的数学内容领域。

参考文献：

[1] 中华人民共和国教育部 . 普通高中数学课程标准（2017 年版 2020 年修订）[S]. 北京：人民教育出版社，2020.

[2] 傅赢芳，谭巍.GeoGebra 在解析几何教学中的应用案例与效果分析[J].数学通报，2018,57(7):25-29.