摘要：数学建模作为连接数学与现实的桥梁，其过程天然蕴含逻辑推理的思维训练，但当前高中数学建模教学存在“重步骤模仿轻思维拆解、重结果呈现轻推理过程、重模型应用轻逻辑验证”的问题，导致学生逻辑推理能力停留在“机械套用”层面。本文基于皮亚杰认知发展理论与数学推理的双重性（演绎与归纳），结合人教版教材教学实践，提出“问题拆解—过程可视化—多维验证”的三阶培养策略，通过具体课例阐述如何在建模全流程中渗透逻辑推理训练，让学生在“发现问题—构建模型—验证模型”的闭环中提升从特殊到一般的归纳能力与从一般到特殊的演绎能力，为高中数学建模教学中逻辑推理能力的落地提供实践路径。

关键词：数学建模；逻辑推理能力；高中数学

一、引言

逻辑推理能力是数学核心素养的核心，而数学建模的“现实问题数学化—数学模型求解—结果现实解释”过程，正是逻辑推理的典型载体。人教版教材中，高一必修第一册“函数的应用”、高二选择性必修第三册“统计案例”等单元均设置了建模内容，但实际教学中，我们常发现学生能套用“收集数据—画散点图—拟合函数”的步骤完成“人口增长模型”，却无法解释“为何选择指数函数而非线性函数”的推理依据；能列出“利润 Σ=Σ 收入 - 成本”的关系式，却忽视“变量取值范围对模型合理性的影响”。这种“知其然不知其所以然”的建模，本质是逻辑推理的断裂——学生缺乏从现实到数学的归纳抽象能力，也缺乏对模型合理性的演绎验证能力。在强调“素养导向”的当下，如何让数学建模教学从“步骤训练”升级为“逻辑推理培养”，成为亟待解决的课题。

二、数学建模与逻辑推理的内在关联及现实矛盾

数学建模的完整流程包含“现实问题抽象（归纳推理）—模型构建与求解（演绎推理）—模型验证与优化（双向推理）”三个阶段，与逻辑推理的“归纳—演绎—辩证”层次高度契合：从具体情境中提炼变量关系（归纳），依据数学原理推导模型表达式（演绎），通过现实数据检验模型适用性（归纳与演绎结合）。

但当前教学中，这一内在关联被割裂，形成三对矛盾：一是问题转化阶段，教师直接给出“需研究的变量”，压缩学生自主归纳变量关系的推理空间，导致归纳能力弱化；二是模型构建阶段，侧重“套用公式”（如直接告知用二次函数模型解决最值问题），忽视“为何选择该模型”的演绎论证过程，导致演绎推理表面化；三是模型验证阶段，仅关注“计算结果是否符合预期”，缺乏“若结果偏离如何修正模型”的辩证推理训练，导致逻辑闭环断裂。这些问题的根源在于将建模视为“操作流程”而非“思维过程”，未能挖掘每个环节的推理训练价值。

三、培养学生逻辑推理能力的三阶教学策略

（一）问题拆解：基于“认知脚手架”理论，引导变量关系的归纳

奥苏贝尔的有意义学习理论指出，当新问题与学生已有经验建立联系时，归纳推理的有效性会显著提升。“认知脚手架”通过将复杂现实问题拆解为阶梯式子问题，降低归纳推理的认知负荷，帮助学生从具体现象中提炼变量间的逻辑关系。

教学“函数的应用”第一节“函数与方程”中的“手机套餐选择问题”为例。教学中不直接给出“资费 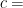月租 + 超出流量费”的关系式，而是设计三级拆解问题：1. 列举“套餐A（月租 58 元，含10GB 流量，超出后1 元/GB）”与“套餐B（月租 88 元，含 30GB 流量，超出后 0.5 元 /GB）”的具体消费案例（如用 15GB 流量时，A 的费用为 58+5×1=63 元，B 的费用为 88 元），让学生观察“流量变化如何影响费用差异”；2. 引导学生用表格整理“流量 x （GB）”与“费用y（元）”的对应关系，标注“ x⩽10 ”“ 10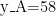′ ”“ _x>30 ”的分段区间；3. 自主归纳不同区间内 y 与 x 的函数关系式（如 x⩽10 时， ，y_B=88）。通过子问题引导，学生在具体案例中逐步归纳出“资费与流量的分段函数关系”，其归纳推理过程不再是“被动接受”，而是“主动发现”，有效解决了“变量关系归纳难”的问题。

（二）过程可视化：基于“双重编码理论”，强化模型构建的演绎推理

双重编码理论认为，语言符号与视觉表象的结合能深化认知加工。将模型构建的演绎过程用“推理流程图”“逻辑树”等可视化工具呈现，可使抽象的演绎步骤显性化，帮助学生厘清“前提—推理—结论”的逻辑链条，避免演绎推理的跳跃与遗漏。

以“成对数据的统计分析”第二节“一元线性回归”中的“身高与体重关系模型”为例。在构建回归直线方程时，采用“四步可视化演绎法”：1. 用散点图直观呈现“身高 ρ_X 与体重 y”的分布趋势，标注“点群大致沿直线分布”（视觉化前提）；2. 用“逻辑树”分解“为何选择线性模型”：假设 1（非线性？但散点无明显曲线趋势）→假设 2（线性？点群分布支持）→结论（优先尝试线性模型）（语言化推理）；3. 用流程图呈现回归直线方程的推导逻辑：“最小二乘法原理” $$ “误差平方和最小”→“参数 a、b 的计算公式” $$ “代入数据求解方程”（步骤化演绎）；4. 用“批注式板书”标注每个步骤的推理依据（如“选择最小二乘法是因为它能最小化整体误差，符合统计学原理”）。通过视觉与语言的双重编码，学生清晰把握了“从数据分布到线性模型再到方程求解”的演绎链条，解决了“模型构建演绎过程模糊”的问题，其演绎推理的严谨性显著提升。

（三）多维验证：基于“批判性思维理论”，发展模型优化的辩证推理

批判性思维理论强调，对结论的质疑与修正能促进高阶思维发展。数学建模的验证环节需引导学生从“肯定”与“否定”双向推理：用现实数据检验模型（正向验证），用极端案例挑战模型（反向质疑），在辩证推理中完善模型，培养“严谨且灵活”的逻辑思维。

教学总复习中的“校园共享单车投放量模型”为例。在构建“投放量 y 与学生人数x、区域面积 s 的多元线性模型”后，设计“三维验证任务”：1. 正向验证：

代入不同年级的学生人数与区域面积数据，计算预测投放量，与实际使用峰值对比，标注“误差在 5% 以内，模型基本适用”；2. 反向质疑：假设“学生放假期间x=0^: ”，模型预测 y=0 ，但实际需保留少量车辆，说明“模型未考虑特殊时段”（发现逻辑漏洞）；3. 优化推理：补充“修正因子 k（特殊时段系数）”，将模型修正为y=ax+bs+k，再次验证时误差降至 2% 。通过“验证—质疑—修正”的辩证推理，学生不仅学会了“用数据支持结论”，更学会了“用逻辑挑战结论”，有效解决了“模型验证缺乏深度”的问题，其逻辑推理的全面性与批判性得到锻炼。

四、结束语

高中数学建模教学中逻辑推理能力的培养，关键在于将“隐性推理”转化为“显性训练”：通过问题拆解，让归纳推理有“阶梯”；通过过程可视化，让演绎推理有“路径”；通过多维验证，让辩证推理有“空间”。这种策略在人教版教材教学中的实践表明，当逻辑推理训练融入建模全流程，学生不仅能“建出模型”，更能“说清道理”，真正实现从“解题”到“解决问题”的思维跃迁，这正是数学建模育人价值的核心所在。

参考文献：

[1] 史宁中，王尚志 . 普通高中数学课程标准（2017 年版 2020 年修订）解读[M]. 北京：高等教育出版社，2020.

[2] 张奠宙，巩子坤 . 数学推理的本质及其教学意义 [J]. 数学教育学报，2022（4）：1-5.

[3] 刘咏梅，陈清华. 基于数学建模的逻辑推理能力培养路径研究[J]. 数学通报，2023（6）：21-25.